V. G. Romanovski
Center for Applied Mathematics
and Theoretical Physics, University of Maribor},
CAMTP, Krekova, 2,
Maribor, SI-2000,
Slovenia.
A. S. Jarrah
New Mexico State University,
Department of Mathematical Sciences,
New Mexico State University,
Las Cruces, NM 88003,
USA
R. Laubenbacher
Virginia Bioinformatics Institute,
1880 Pratt Drive Blacksburg,
VA 24061, USA
reinhard@almaren.bioinformatics.vt.edu
The problem of small limit cycles bifurcations
(the cyclicity problem) is considered for the system with homogeneous
cubic nonlinearities
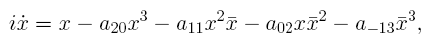
and for the cubic system
where a
In the case of the second system it appears the ideal of focus quantities is not a radical one. Nevertheless using the monoid structure of the focus quantities we are able to find a basis of the ideal and to solve the cyclicity problem for "almost all" values of parameters of the system.