ГИБРИДНЫЕ СИСТЕМЫ И РАНДОМИЗИРОВАННЫЕ ИЗМЕРЕНИЯ В НЕРАВНОВЕСНЫХ ПРОЦЕССАХ

О.H.Граничин (докт. физ.-мат. наук), Т.А.Хантулева (канд. физ.-мат. наук),

Санкт-Петербургский государственный университет

1. Математические модели процессов и измерений

Для многих практических задач управления теория до сих пор не может предложить удовлетворительных решений. Среди них: проблемы динамически реконфигурируемого интеллектуального управления, асинхронного управления, управления через Интернет, управления командой роботов, программирование системы управления бактерией и многие другие. Одна из основных трудностей связана с недостатками в подходах к составлению формального математического описания задач. Традиционные методы описания динамических систем предполагают выбор некоторого пространства состояний с границей и составление уравнения динамики

для зависящей от времени переменной состояния _. Управляющая переменная характеризует внешние воздействия на систему (играет роль «посредника» с внешним миром). Вид уравнений динамики и граничных условий обычно задается с точностью до некоторого конечномерного набора констант , называемого параметрами системы. После удачного и обоснованного выбора математической модели одной из основных задач, возникающих при анализе реальных динамических систем, является получение или уточнение информации о реальных параметрах системы (идентификация системы). Эта информация в дальнейшем обычно используется при прогнозировании поведения системы или при формировании закона управления. Наряду с описанием динамики процесса в системах управления выбирают ту или иную модель наблюдений. Любые измерения дают всегда значения величин, заведомо усредненные как по некоторой пространственной области, так и по некоторому промежутку времени. Обычно набор наблюдений y может быть представлен как

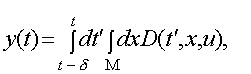
где М - подмножество пространства состояний (обычно ), интервал времени определяются характеристиками регистрирующих приборов. После дискретизации модели наблюдений обычно удается получить выражение

в котором понимается как стандартная ошибка в наблюдении (помеха), первая часть которой обычно называется статистической погрешностью, а вторая - систематической (погрешностью модели). За последние пятьдесят лет вопросам идентификации систем было посвящено множество работ. В физике проблемы восстановления параметра по данным наблюдения называют обратными задачами. В большинстве рассматриваемых в литературе методов предполагается, что статистическая погрешность либо мала, либо обладает какими-либо «полезными» статистическими свойствами, либо хотя бы ограничена, а вопрос о наличии систематической погрешности вообще не рассматривают, предполагая возможность ее устранения на этапе выбора модели или планирования эксперимента (см., например, [1]). В нелинейных моделях решение задачи идентификации осложняется тем, что очень часто траектории нелинейных систем при малом расхождении в начале за сравнительно небольшой промежуток времени успевают значительно «разбежаться». Этот эффект лежит в основе «хаотического» описания поведения динамических систем (см., например, обзор [2]). Модели с «хаосом» дают много возможностей для приложений современных математических теорий, чрезвычайно содержательных и интересных, но, к сожалению, с их использованием далеко не всегда удается приблизиться к решению задачи идентификации. Вообще говоря, выход на хаос предполагает переход описания системы на другой, более грубый уровень – макроскопический, когда средние значения распределены в пространстве. Плотности распределения удовлетворяют уравнениям баланса, которые вблизи термодинамического равновесия являются дифференциальными уравнениями в частных производных. В классической механике сплошной среды известно, что на малых характерных временах и небольших внешних воздействиях эти уравнения гиперболического типа, а на больших временах при длительных и интенсивных нагружениях уравнения баланса параболического типа, описывающие диффузионные процессы переноса. Быстропротекающие и сильноградиентные процессы, сочетающие как волновые, так и диффузионные свойства переноса, как показывают теоретические и экспериментальные исследования, не описываются дифференциальными уравнениями классической механики сплошной среды.. В неравновесной статистической механике получены интегро-дифференциальные уравнения баланса, перекрывающие весь диапазон режимов от волнового при незатухающей памяти и полной пространственной корреляции до гидродинамического в пределе полной потери памяти о начальном состоянии системы и затухания пространственных корреляций. Однако, такое описание является заведомо неполным и требует структурирования этой неопределенности.

В реальных системах число степеней свободы бесконечно, и гипотеза о конечномерности фазового пространства правомерна только тогда, когда из всех степеней свободы выделяется конечное, обычно небольшое, число характеристик порядка, определяющих поведение системы в конкретных условиях с достаточной точностью. Наиболее трудными для формального описания являются динамические, «переходные» процессы в системах, возникающие при быстром изменении «внешних» условий. Обычные подходы к описанию таких неравновесных процессов неэффективны, поскольку сама структура пространства состояний зависит от времени. Экспериментальные наблюдения за протеканием неравновесных процессов подтверждает зарождение в системе новых структур мезоскопического (промежуточного между микро и макро) масштаба, которые в значительной степени и определяют динамическое изменение типа формальной модели. Примерами такого рода структурообразования могут служить: кластеризация в потоках концентрированных дисперсных смесей, образование многомасштабных вихревых структур в турбулентных течениях жидкости и пластических течениях твердых материалов при импульсном нагружении, а также иерархии структур в живых системах (см., например, [3-4]). В настоящее время известно, что синергетические процессы формирования динамических структур мезоскопического масштаба в открытых термодинамических системах связаны с возникновением информационно-управленческой обратной связи, внутреннего управления, которое вместе с внешним управлением через наложенные на систему граничные условия и приводит к дискретизации пространства и времени неравновесной системы.. При этом физическими носителями информации являются элементы динамических структур. Другими словами, для адекватного описания динамики поведения таких систем недостаточно выбрать ту или иную модель типа (1) с фиксированным числом параметров порядка и привязанную только к одному масштабному уровню. Будем рассматривать новый класс моделей, предположив, что структура пространства состояний может меняться со временем. Более точно, предположим, что задано некоторое множество возможных структур пространства состояний. Обозначим текущую структуру пространства состояний через и - текущее пространство состояний. Вместо уравнения (1) будем рассматривать

где L – некоторое пространство, может быть и бесконечномерное, в которое вкладываются все промежуточные пространства состояний. Как правило, структура пространства состояний изменяется медленнее динамики состояний и описание пространств существенно проще L. Типичными является выбор конечномерных пространств с невысокой размерностью. При этом физические соображения подсказывают интегральную зависимость структуры пространства состояний от всей предыстории развития процесса

s(t) =

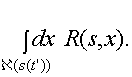
В теории управления такого типа модели для описания сложных динамических процессов появились недавно и системы такого типа называют «гибридными» [5]. В этом названии подчеркивается двухуровневая специфика описания. Один уровень – динамика описания в некотором пространстве состояний («быстрый» процесс), а второй уровень – динамика изменения структуры пространства состояний («медленный» процесс).

Рассмотрение более общей схемы (1’) с неизбежностью приводит к тому, что становится достаточно трудно в формуле (3) систематическую погрешность исключить из рассмотрения. Традиционные методы для этого не годятся, так как по логике составления новой модели невозможно с уверенностью говорить о том, какова же в данный момент структура пространства состояний, и соответственно предпринимать те или иные меры, направленные на «погашение» систематической погрешности. Таким образом, необходимость учета систематической погрешности измерения является специфической особенностью неравновесных процессов, отраженных в моделях с переменной структурой пространства состояний.

2. Рандомизация наблюдений

Как же все-таки поступать при решении обратных задач в физике? Можно ли вообще говорить о решении задач идентификации при наличии произвольной систематической погрешности? Наверное, ответить на эти вопросы можно, только переосмыслив традиционного понятия измерения (контроля). Целью этой работы является демонстрация возможности контроля неравновесных процессов без стандартных предположений о помехах наблюдений, что достигается за счет рандомизации процесса наблюдения («управляемых» или «активных» наблюдений). Возможностям оценки неизвестных параметров при почти произвольных помехах посвящена монография [6].

Рассмотрим простейший пример привычной схемы обработки результатов измерений. Пусть нас интересует некоторая характеристика исследуемого процесса , значение которой надо уметь контролировать. Предположим, что ее можно определить на основе исследования передаточной функции от функции u, задающей граничные условия, к измерениям y. Для упрощения рассмотрим простейший скалярный случай и =. Для модели измерений (3) в этом случае получаем

y = u + помеха наблюдения.

Если мы имеем дело с системой, состояние которой на данной стадии можно считать установившимся, то для определения неизвестного значения можно воспользоваться обычной методикой, состоящей в проведении серии опытов и усреднении данных измерений. Эта методика работает при предположении о независимости и центрированности последовательности помех наблюдений, т.е. при статистических «хороших» помехах. При невозможности многократно повторить измерения, например, в неравновесных динамических процессах, при высоком уровне помех наблюдения полученное в результате эксперимента значение y фактически ничего не говорит о реальном значении характеристики . Другими словами, простое усреднение результатов измерений не годится при наличии систематической погрешности в модели. Как ни странно, но одним из способов устранения негативного влияния систематической погрешности является использование предложенных в [6-9] рандомизированных алгоритмов для активных измерений. Предположим, что в моменты времени n=1,2,… известны некоторые пробные воздействия на систему u₁, u ₂,…, совокупность которых обозначим {u_n}. Для наблюдаемых величин {y_n} можно записать безразмерные соотношения:

y_n = u _n + w_n , n=1,2,…,

в которых w₁, w₂,…- возмущающее воздействия (помехи измерения). Пусть пробное воздействие {u_n} имеет статистическую природу, представляя собой последовательность независимых между собой ограниченных случайных величин с известным ненулевым средним значением ≠0, положительной ограниченной дисперсией >0 и ограниченным четвертым моментом. Восходящая к работам Гаусса и Лежандра идея метода наименьших квадратов, базируется на усреднении n последовательных данных наблюдения, умноженных на соответствующие значения пробных воздействий. При случайных независимых помехах наблюдения с ограниченными вторыми статистическими моментами, в силу усиленного закона больших чисел, последовательность оценок обыкновенного метода наименьших квадратов (МНК) сходится при n →∞ с вероятностью единица к значению , где M_v - среднее значение возмущающих воздействий. Следовательно, при достаточно большом количестве наблюдений и известной величине M_v можно говорить о решении поставленной задачи об определении значения . При неизвестном и значительном по абсолютной величине значении Mv или при неизвестной неслучайной последовательности помех наблюдения этот классический алгоритм не годится. Домножим на Δ_n =(u_n - ) обе части соотношения, определяющего наблюдаемые величины y_n, и, произведя несложные преобразования, получаем

Δ_n y_n = Δ_n² + Δ_n + Δ_n w _n .

Просуммировав первые N измерений и усреднив, имеем

Σ Δ_ny_n /N = Σ Δ_n²/N + Σ Δ_n/N + Σ Δ_n w _n/N.

Первое и второе слагаемое в правой части при сделанных предположениях, в силу усиленного закона больших чисел, при n →∞ с вероятностью единица стремятся к и нулю соответственно. Можно показать, что по той же причине и последнее слагаемое с вероятностью единица при n →∞ стремится к нулю. Отсюда следует, что при ≠ последовательность оценок {}, формируемых по правилу

сходится при n →∞ с вероятностью единица к .

Типичное поведение последовательности оценок {} при различных типах погрешностей показано на рис.1.

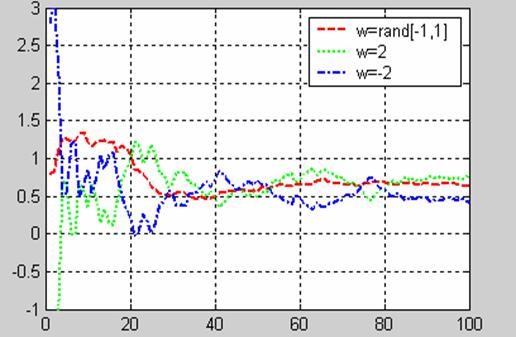
Рис.1. Последовательности оценок {}

Существенным ограничением рассмотренного способа является то, что результат о состоятельности оценок носит асимптотический характер. Вместе с тем, в первой части работы как раз указывалось на то, что в неравновесных задачах со временем структура пространства состояний может измениться, а, значит, не естественно предполагать возможность длительного процесса наблюдения за системой. Кроме того, само использование управляющих воздействий может «раскачать» систему и тип ее возможного описания изменится. В [9] предлагается оригинальный способ оценивания передаточной функции от u к y на основании конечного числа наблюдений (правда, при стандартных предположениях о помехах наблюдения). Но на самом деле этот способ остается работоспособным и при произвольных помехах. Это позволяет надеяться на то, что в ближайшем будущем будет разработана методика оценивания неизвестных параметров, дающая содержательные ответы при произвольных помехах и при конечном числе наблюдений.

Итак, традиционное предположение о независимости и центрированности помех наблюдения в серии экспериментов может быть существенно ослаблено. А, значит, при управлении в неравновесных, быстро меняющихся условиях теоретически возможно за счет рандомизации компенсировать негативное влияние систематических погрешностей. Стоит отметить, что даже быстрое протекание переходных процессов в реальных системах, описываемых на макроуровне, не происходит мгновенно. Например, фронт волны, распространяющейся в металле после высокоскоростного удара, проходит фиксированную точку за время порядка 10⁻⁷c. Современные измерительные средства вышли на уровень нанотехнологий (10⁻⁹), и состояние развития микропроцессорной техники вполне позволяет говорить о возможности в реальном времени отслеживать некоторые характеристики процесса. В частности, это может позволить выделить из теоретически предсказанного «грубого» множества возможных траекторий (или типов моделей) ту единственную, которая реализовалась в конкретном эксперименте, или, по крайней мере, существенно сократить множество неопределенностей. Далее полученную информацию целесообразно использовать в контуре управления. Конечно, эти результаты измерений не будут повторяться от одного эксперимента к следующему.

Литература

[1] Льюнг Л., Седерстрем T. «Идентификация систем: теория для пользователя».

М.: Hаука, 1991, 431 с.

[2] Андриевский Б.P., Фрадков А.Л. // АиТ. 2003. №5, №6.

[3] Хантулева Т.А., Мещеряков Ю.И. “Роль неравновесных процессов нелокальности и памяти в структурообразовании динамически деформируемых сред”. Части 1,2. Известия ВУЗов «Физика». 2000. 4. с 62-73, 9, с. 66-75.

[4] T.A.Khantuleva. “The Shock Wave as a Nonequilibrium Transport Process.” Chapter 6 in collective monograph “High-Pressure Compression of Solids VI: Old Paradigms and New Challenges”(Y.Horie, L.Daison, N.N.Thadhani, Eds.), Springer-Verlag, New York, 2003. P. 121-161

[5] G.Pola, M.L.Bujorianu, J.Lygeros, M.D.Di Benedetto. “Stochastic Hybrid Models: an Overwiew”.

[6] Граничин О.Н., Поляк Б.Т. “Рандомизированные алгоритмы оптимизации и оценивания при почти произвольных помехах”. М.: Наука, 2003, 291с.

[7] Граничин О.Н. “Алгоритм стохастической аппроксимации с возмущением на входе для идентификации статического нестационарного дискретного объекта” // Вестник Ленингр. ун-та, cер.1, 1988, вып.3(15), с.92-93.

[8] Goldenshluger A.V., Polyak B.T. “Estimation of regression parameters with arbitrary noise” // Mathematical Methods of Statistics, 1993, vol.2, No.1, p.18-29.

[9] Граничин О.Н., “Оценивание параметров линейной регрессии при произвольных помехах” // АиТ. 2002. №1. С.30-41.

[10] M.C. Campi, E. Weyer “Identification from a finite data set: Construction of confidence regions with guaranteed probability”