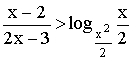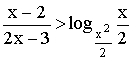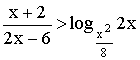Матмех. Региональная олимпиада по математике 20 апреля 2003 года.
Задачи
Первый вариант
-
Укажите все квадратичные трехчлены x2+ax+b (a, b - вещественные числа), такие,
что x6+ax3+b делится на x2+ax+b без остатка.
-
Сумма конечной убывающей арифметической прогрессии, одним из членов которой является -1, равна 0.
Найдите ее разность, если известно, что произведение 7-го и 13-го членов равно 1.
-
Решите неравенство:
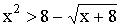
- Решите неравенство:
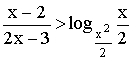
-
Решите уравнение:
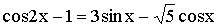
-
Окружность, построенная на стороне AB остроугольного треугольника ABC
как на диаметре, пересекает в точке K высоту, опущенную из вершины C.
Докажите, что CK . HP = HK . KP,
где P - основание высоты, а H - ортоцентр.
-
В равнобедренной трапеции ABCD основания AD=33 и BC=63.
Найдите радиус окружности, описанной вокруг трапеции, если известно, что отношение радиусов окружностей,
вписанных в треугольники ABD и ABC, равно 2/3.
Второй вариант
-
Укажите все квадратичные трехчлены x2+ax+b (a, b - вещественные числа),
такие, что x6+ax3+b делится на x2-ax+b без остатка.
-
Сумма конечной возрастающей арифметической прогрессии, одним из членов которой является 1, равна 0.
Найдите ее первый член, если известно, что произведение 4-го и 14-го членов равно 1.
-
Решите неравенство
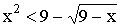
- Решите неравенство
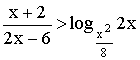
- Решите уравнение
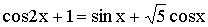
-
Перпендикуляр, восстановленный из точки K, лежащей на гипотенузе AB прямоугольного треугольника ABC,
пересекает катет AC в точке N и продолжение катета BC в точке D.
Докажите, что MK2 = DK . KN,
где M - точка пересечения отрезка KD с окружностью, описанной около треугольника ABC.
-
В равнобедренной трапеции ABCD диагональ BD=15 и боковая сторона CD=13.
Найдите площадь трапеции, если известно, что отношение радиусов окружностей, вписанных в треугольники
ABC и ABD, равно 3/8.