Решения задач олимпиады 2001г.

Вариант 1
  1. а) Ответ: 33.

    2. Пусть  - длины сторон треугольника. Надо подсчитать число точек, натуральные координаты (x,y) которых удовлетворяют неравенствам , т.е. , откуда 
    В частности, , откуда . Теперь проще всего осуществить тривиальный перебор. Именно, если y = 11, то ;  имеем 2 варианта.При y = 12:  - 4 варианта; и так далее.
    Наконец при y = 19 x = 2.

    б) Если x1 - меньший корень, то значение p(x1 + 1), ... p(x1 + 2000) отрицательны, поэтому квадратичный многочлен, стоящий в левой части уравнения, имеет вещественные корни.

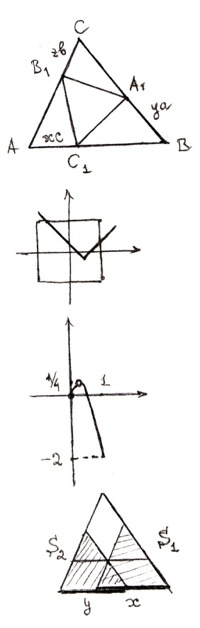
    в) Обозначим через x, y, z отношения длин отрезков AC1 : AB, BA1 : BC и CB1 : AC. Тогда

    г) Ответ: 1/27, так как меньшая пирамида гомотетична большей с коэффициентом -1/3.

  2. а) Ответ:  (см. рис.)

    3. б) Ответ: При p>0 это множество, заданное неравенствами
    Действительно, дискриминант должен быть неотрицателен, а значение многочлена при x = p - положительно.

    в) Ответ: . Положим 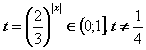, при этом  (см. рис.).
    г) Ответ: восемь решений. Достаточно положить
    ,  и исследовать функцию ,
    которая монотонно меняется между 1 и 2-999 на каждом из отрезков .

  3. а) Нетрудно видеть, что f(x + 4a) = f(x).

    4. б) Ответ: Нет, не может.
     
Вариант 2
  1. а) Ответ: 44

    2. в) Если S1 = x2S и S2 = y2S (см. рис.), то S3 = (2 - x - y)2S.
    г) Пусть (x0, y0, z0) - заданная точка, a, b, c - координаты точек пересечения плоскости с полуосями. Тогда
    Откуда . Причем равенство достигается в том случае, когда
  2. а) Ответ: (x, y) = (3, -2); (0, -3).

    3. б) Ответ: При p > 0 это множество точек, заданных неравенствами -2p2 < q < 0   и уравнением 4q = p2.
    в) Ответ: (-8; 0).
    г) Ответ: Четыре решения.