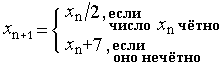Задачи Олимпиады для школьников (23 апреля 2000 г.)
Вариант 1
Задание 1.
a) Существует ли геометрическая прогрессия, среди членов которой имеются
числа 2, 3 и 5?
б) Решите уравнение [2 cos 3x] = 2 sin2x
(здесь [..] - это целая часть числа, т.е. наибольшее целое число,
его не провосходящее).
в) Найдите количество лежащих на кривой x2
- y2 = 2000 точек плоскости, кординаты которых
суть целые числа.
г) Два шахматиста играют матч до первой победы. Известно, что во встречах
друг с другом каждый из них, играя белыми фигурами, побеждает с вероятностью 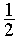 ,
а проигрывает с вероятностью
,
а проигрывает с вероятностью 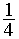 (тем самым с вероятностью
(тем самым с вероятностью 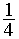 в каждой из партий фиксируется ничья). Если в 40 партиях матча будет зафиксирована
ничья, то для определения победителя кидают жребий. Оцените (с разумной
точностью) шансы на выигрыш того игрока, с хода которого начнется матч).
в каждой из партий фиксируется ничья). Если в 40 партиях матча будет зафиксирована
ничья, то для определения победителя кидают жребий. Оцените (с разумной
точностью) шансы на выигрыш того игрока, с хода которого начнется матч).
Задание 2.
а) Решите неравенство: 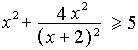 .
.
б) Решите уравнение: 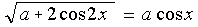 .
.
в) Внутри угла величиной 600 с вершиной в точке A
на расстоянии 4 от нее расположена точка M.
Найдите расстояние между основаниями перпендикуляров, опущенных из точки
M
на стороны этого угла.
г) Сколько сторон имеет сечение куба ABCDA'B'C'D'
плоскостью, проходящей через точки 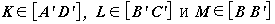 ,
которые делят эти отрезки в, соответственно, отношениях 16:9, 2:3, 1:2
(считая от вершины, указанной первой)?
,
которые делят эти отрезки в, соответственно, отношениях 16:9, 2:3, 1:2
(считая от вершины, указанной первой)?
Задание 3.
Последовательность {xn}, начальный член x0
которой - натуральное число, задана соотношениями
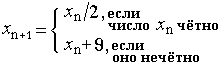
а) Найдите все периодические последовательности данного вида.
б) Докажите, что всякая последовательность данного вида имеет периодический
"хвост", т.е. для нее найдутся такие натуральные числа N
и t, что xn+t =
xnдля
всякого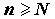 .
.
Задачи Олимпиады для школьников (23 апреля 2000 г.)
Вариант 2
Задание 1.
a) Существует ли геометрическая прогрессия, среди членов которой имеются
числа 3, 7 и 10?
б) Решите уравнение [2 sin 3x]
= -2 sin 2x (здесь [..] - это целая часть числа,
т.е. наибольшее целое число, его не превосходящее).
в) Найдите количество лежащих на кривой x2 - y2
= 1944 точек плоскости, кординаты которых суть целые числа.
г) Два шахматиста играют матч до первой победы. Известно, что во встречах
друг с другом каждый из них, играя белыми фигурами, побеждает с вероятностью 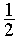 ,
а проигрывает с вероятностью
,
а проигрывает с вероятностью 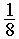 (тем самым с вероятностью
(тем самым с вероятностью 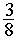 в каждой из партий фиксируется ничья). Если в 80 партиях матча будет зафиксирована
ничья, то для определения победителя кидают жребий. Оцените (с разумной
точностью) шансы того игрока, с хода которого начнется этот матч.
в каждой из партий фиксируется ничья). Если в 80 партиях матча будет зафиксирована
ничья, то для определения победителя кидают жребий. Оцените (с разумной
точностью) шансы того игрока, с хода которого начнется этот матч.
Задание 2.
а) Решите неравенство: 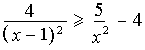
б) Решите уравнение: корень квадратный из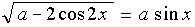 .
.
в) На сторонах угла величиной 1200
с вершиной в точке A на расстоянии 4
друг от друга лежат точки K и L.
Пусть M- точка пересечения восстановленных
в точках K и
L
перпендикуляров к соответствующим
сторонам углам. Найдите расстояние от M до
А.
г) Сколько сторон имеет сечение куба ABCDA'B'C'D' плоскостью, проходящей
через точки 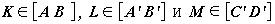 ,
которые делят эти отрезки в, соответственно, отношениях 1:4, 11:4, 8:7
(считая от вершины, указанной первой)?
,
которые делят эти отрезки в, соответственно, отношениях 1:4, 11:4, 8:7
(считая от вершины, указанной первой)?
Задание 3.
Последовательность {xn}, начальный член x0
которой - натуральное число, задана соотношениями
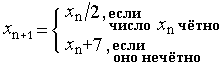
а) Найдите все периодические последовательности данного вида.
б) Докажите, что всякая последовательность данного вида имеет периодический
"хвост", т.е. для нее найдутся такие натуральные числа N и t,
что xn+t = xn для всякого n>N.
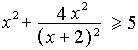 .
.
![]() ,
которые делят эти отрезки в, соответственно, отношениях 16:9, 2:3, 1:2
(считая от вершины, указанной первой)?
,
которые делят эти отрезки в, соответственно, отношениях 16:9, 2:3, 1:2
(считая от вершины, указанной первой)?
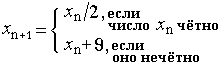
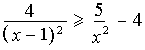
![]() ,
которые делят эти отрезки в, соответственно, отношениях 1:4, 11:4, 8:7
(считая от вершины, указанной первой)?
,
которые делят эти отрезки в, соответственно, отношениях 1:4, 11:4, 8:7
(считая от вершины, указанной первой)?