, т.е. 3n
= 5k2n-k,
что невозможно.
Ответы к задачам варианта 1
Задание 1.
а). Ответ: нет, не существует.
Действительно, если 3=2qkи5=2qn,
то , т.е. 3n
= 5k2n-k,
что невозможно.
б) Ответ:
; 
; 
; 
, 
.
Так как левая часть уравнения может принимать
лишь значения 
, то осуществим
перебор.
А) Пусть a =
2.
Тогда sin 2x
= 1, откуда 
. Имеем 
,
так что
[2cos 3x]<2 и этот случай невозможен.
Б) Пусть a =
1: 
, 
или 
. В первом случае 
.
Из значений 
нам подходит
только 
,
поэтому число k должно
быть четным. Во втором случае, наоборот, n
нечетно. Поэтому 
или 
.
В) Пусть a
= 0: 
, 
.
Таким образом, 
.
Г) Пусть a=
-1: 
,
или 
. В этом случае
[2cos 3x]
= -2; 1, так что решений нет.
Д) Наконец, пусть a=
-2.Тогда 
, а число k
должно быть четно. Таким образом, 
.
в) Ответ: 24 точки.
Имеем: (x
+ y)(x- y) = 2453.
Так как числа x
+ y и x
- y, будучи целыми имеют одинаковую
четность, то x = 2a
и
y = 2b,
где ab =2253.
Таким образом, количество решений данного уравнения совпадает с количеством
чисел вида 2s5t,
s=
0, 1, 2,
t = 0, 1, 2, 3.
г) Ответ: шансы первого игрока
3:2, так как вероятность его
победы почти равна 
.
Вероятность того, что все 40 партий закончатся вничью почти равна
4-40 = 2-80 < 10-24, поэтому будем считать, что матч продолжается до первой победы. Вероятность победы игрока, который в первой партии играет белыми фигурами, равна сумме ряда
p + qr + pr2 + qr3 + ... =(p + qr)(1 + r2 + r4
+ ...) = 
,
здесь 
, 
-
вероятности
ничьи.
Второе решение: Искомая вероятность является решением уравнения
а) Ответ: 
.
После стандартных преобразований получим
неравенство 
.
б) Ответ:
, 
,
при 
;
, ,
при 
,
, при 
;
; 
,
при 
.
получаем уравнение 2|cos x| = 0,
т.е. 
. При имеем 
, .
Вообще, 
есть
решение только при . Поэтому
в дальнейшем будем считать, что 
.
После замены 
получим уравнение 
,
откуда 
. Случай
уже исследован, так что 
.
Из условий 
получаем, что 
.
Таким образом, 
при 
и 
при 
.
в) Ответ:
.
Имеем: 
,
так что 
(см. Рис. 1).
г) Ответ: пять сторон.
Если расположить начало системы координат
в вершине С куба, а ее оси направить по ребрам, то из условий
на точки K, L, M следует,
что их координаты равны 
, 
, 
.
Для определения коэффициентов уравнения 
плоскости (KLM) получаем
систему
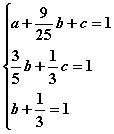
Откуда 
, 
и 
. Найдем координаты точки
P
пересечения
прямой
AA' и плоскости
KLM
: x = y =1,
так что 
. Для контроля укажем
отношения, в которых точки Q
и S плоскости делят,
соответственно, ребра AB
и AD куба AQ
:
QB= 1 : 5, AS : SD = 1 : 25.
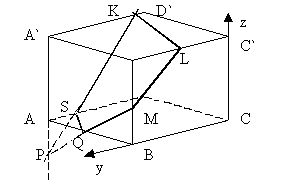
Рис.1.
Задание 3.
а), б) Ответ:14 последовательностей с начальными членами из множества X0 = {1, 2, ..., 9, 10, 12, ... ,18}.
То, что эти числа порождают периодические
последовательности, проверяется непосредственно. 
{11, 13, 15, 17},
X0
, поэтому такая последовательность непериодична, но ее хвост {
}
периодичен. Для завершения доказательства достаточно показать, что во всякой
последовательности найдется член 
.
Предположим, что это не так. Если 
то, как нетрудно видеть, 
,
однако строго убывающей последовательности состоящей из натуральных чисел,
не существует.
Ответы к задачам варианта 2
Задание 1.
а) Ответ: нет, не существует.
б) Ответ:
; 
; 
; 
,.
в) Ответ: 24 точки.
г) Ответ: шансы первого игрока - 7:4, так как вероятность его победы почти равна 
.
Задание 2.
а) Ответ: 
.
б) Ответ:
, ,
при 
;
, ,
при ,
, при ;
; 
]
при .
.
г) Ответ: пять сторон.
В системе координат с началом в вершине
B
куба плоскость (KLM)
задается уравнением 
. Точка
пересечения P этой плоскости
с прямой CD имеет координаты
(1, 
, 0), а точки Q
и S пересечения с ребрами
AD
и DD' делят
их в отношении 3:1 и 1:7, соответственно.
Задание 3.
а) Ответ: 11 последовательностей
с начальными членами из множества
{1, 2, ..., 7, 8, 9, 10, 12,14}.