Лекция 6: Теория вероятностей. Случайные величины
Предмет лекции
При реальном использовании теории вероятностей к пространству элементарных событий
никогда не обращаются. Это понятие нужно для теоретических обоснований вероятностных схем.
Наиболее часто рассматриваются случайные схемы, в которых событием является появление какого-то
числа. Для таких схем вводится понятие случайной величины . Этому понятию и будет
посвящена наша лекция. Мы рассмотрим случайные величины, способы их задания (так называемые
законы распределения ), числовые характеристики случайных величин,
а также наиболее часто встречающиеся законы распределения.
|
Случайная величина
Случайной величиной называется отображение множества элементарных событий в множество
вещественных (или целых) чисел
ξ: S ® R.
Предполагается такая схема: в результате случайного эксперимента
выбирается одно из элементарных событий, по нему вычисляется значение функции, и это значение
наблюдается. Упомянутое отображение определяет вероятности появления тех или иных значений
случайной величины.
Например, пусть множество элементарных событий состоит из двухкратных бросаний игральной кости, что дает
36 элементарных исходов. Пусть функция ξ определена как сумма значений, выпавших
на костях. Очевидно, такая случайная величина может принимать значения от 2 до 12. При этом значению
2 соответствует одно элементарное событие, а, скажем, значению 9 — четыре:
(3,6), (4,5), (5,4) и (6,3).
Обычно наблюдаются и изучаются не элементарные события, множество которых нам совершенно неизвестно,
а именно случайные величины. Чтобы задать их вероятностное поведение, нужно задать вероятности того, что
случайная величина принимает то или иное значение. Рассмотренный нами пример случайной величины мы сможем
опеределить так:
| x |
2 | 3 | 4 | 5 | 6 |
7 | 8 | 9 | 10 | 11 | 12 |
| P(x) |
1/36 | 2/36 | 3/36 | 4/36 | 5/36 |
6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
Попробуйте сами составить таблицу вероятностей суммы очков трех бросаний игральной кости.
Определение вероятностей, с которыми случайная величина принимает свои значения называется
ее законом распределения .
|
Функция распределения случайной величины
Одним из важнейших способов задания закона распределения — это задание
функции распределения .
Функцией распределения случайной величины ξ называется функция
Fξ(x) =
P(ξ < x) ,
−∞ < x < ∞ .
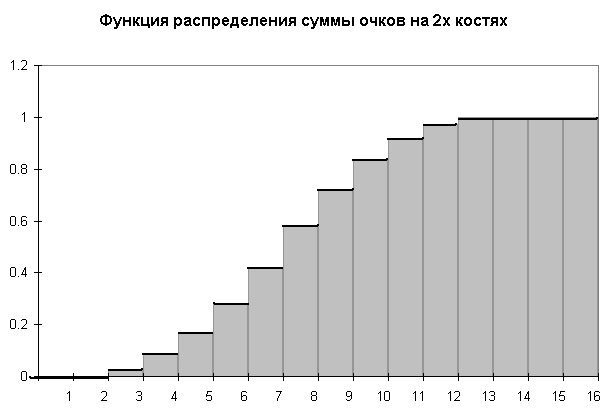 На рисунке изображена
На рисунке изображена
функция распределения
случайной величины, рассмотренной в качестве примера.
Для наглядности область под графиком функции закрашена
в серый цвет. Отчетливо видно, что эта функция монотонно неубывающая и кусочно-постоянная.
Она имеет скачки в тех точках, которые соответствуют значениям, принмаемым с положительной вероятностью.
Такая функция распределения частно называется интегральной . Когда она непрерывна и у нее
есть производная, то эту производную часто называют плотностью распределения .
Если функция распределения, как в нашем примере, кусочно-постоянна, но роль плотности может
играть набор скачков.
Задавать произвольную функцию распределения дело хлопотное. Для упрощения используются два подхода.
Во-первых, часто можно ограничиться некоторыми очень простыми численными характеристиками случайной величины.
Во-вторых, имеются часто встречающиеся классы вероятностных распределений, и часто по каким-то
«модельным» соображениям можно понять, к какому классу принадлежит данное распределение.
В этом случае достаточно только задать параметры этого распределения.
Эти подходы мы сейчас и рассмотрим.
|
Характеристики случайных величин
Пусть задана случайная величина ξ , принимающая конечное число значений
a1 ,
a2 , ...
ak
с вероятностями
p1 ,
p2 , ...
pk
Математическим ожиданием этой случайной величины называется сумма
Eξ = Σi
О 1:k piai.
Как определяется математическое ожидание для более общего случая, нужно говорить отдельно:
используются интегралы, но вас уже учили, что интеграл определяется через интегральные
суммы, и для случайных величин можно вводить близкие к ним дискретные случайные величины,
математические ожидания которых будут играть роль интегральных сумм для математического
ожидания исходной случайной величины.
Математическое ожидание, как видно из этой формулы, можно трактовать как центр тяжести
набора масс pi , сосредоточенных в точках
ai . Естественно,
что и свойства его нам хорошо знакомы как свойства центра тяжести:
- если случайная величина с вероятностью 1 принимает значение
a , т. е.,
если k = 1 , то Eξ = a,
- если
η = cξ , где c — постоянная, то
Eη = cEξ ,
- для любых
ξ и η выполняется
E(ξ + η) = Eξ + Eη ,
Дисперсией случайной величины называется математическое ожидание квадрата отклонения
этой случайной величины от ее математического ожидания.
Это определение сначала вызывает тихий ужас. На самом деле, это очень удобное словесное описание формулы.
Слова математическое ожидание означают, что мы должны написать
Dξ = E (...)
квадрата уточняет
Dξ = E (...)2
отклонения относится уже к выражению в скобках
Dξ = E (... − ...)2
случайной величины от ее математического ожидания завершает написание формулы
Dξ = E
(ξ − Eξ)2
Дисперсию можно трактовать как момент инерции
того же набора масс относительно его центра тяжести. Ее
свойства нам тоже хорошо знакомы:
- если случайная величина с вероятностью 1 принимает значение
a ,
то Dξ = 0,
- если
η = cξ , где c — постоянная, то
Dη = c2Dξ .
- Хотелось бы иметь и равенство
D(ξ + η) = Dξ + Dη , но оно верно только для случая
независимых случайных величин .
Случайные величины ξ и η называются независимыми ,
если для любых a и b независимы события
{ξ < a} и {η < b} .
Легко убедиться в том, что если мы суммируем n независимых и одинаково распределенных
случайных величин с математическим ожиданием a и дисперсией b ,
то для их суммы математическое ожидание и дисперсия равны
соответственно n a и n b , а для среднего арифметического —
соответственно a и b/n .
Значит, если мы хотим оценить какое-то
число, которое является математическим ожиданием некоторой случайной величины, мы можем устроить
случайное испытание — наблюдать много раз эту случайную величину и вычислить среднее
арифметическое. Его разброс вокруг истинного значения будет уменьшаться с ростом числа наблюдений:
сто раз измеришь — в десять раз уменьшится (так как важна не сама дисперсия, а корень из нее).
Используются и другие характеристики, но эти самые важные. Сейчас мы рассмотрим некоторые важные типы распределений
и каждый раз будем указвать их математическое ожидание.
|
Типы распределений
Равномерное распределение
Случайная величина распределена равномерно в промежутке [a,b] , где a < b ,
если ее функция распределения F(x) равна 0 при x < a ,
1 при x > b
и меняется линейно от 0 до 1 при a < x < b .
Математическое ожидание такой случайной величины равно (a + b)/2 , а дисперсия —
(b − a)/12 .
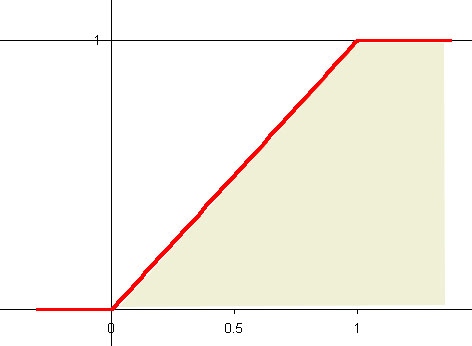 На рисунке показан график этой функции распределения для
На рисунке показан график этой функции распределения для a = 0 и b = 1 .
Этот закон распределения нам очень важен, так как все стандартные датчики случайных величин
(псевдослучайные числа ) моделируют именно такие случайные величины, а из них уже
и создаются нужные нам случайные величины.
|
Показательное распределение
Случайная величина распределена показательно или экспоненциально ,
если она неотрицательна и F(x) = 1 − exp(−λ x) ,
где λ — положительная константа.
Математическое ожидание такой случайной величины равно λ− 1 , а дисперсия —
λ− 2 .
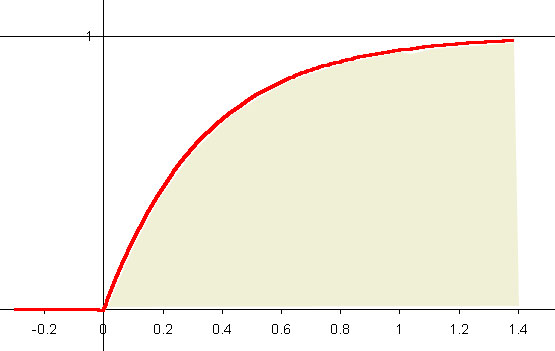 На рисунке показан график этой функции распределения для
На рисунке показан график этой функции распределения для λ = 3 .
Этот закон распределения нам часто встречается в приложениях, особенно в радиотехнических и
коммуникационных. В частности, часто предполагается, что время разговора двух абонентов распределено
по показательному закону.
|
Нормальное распределение
Это самое популярное из стандартных распределений вероятности, и на первый взгляд может
показаться странным, что наиболее распространена такая сложная формула .
Случайная величина распределена нормально или по Гауссу , если
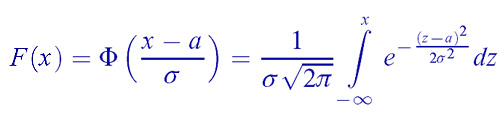

Эта функция зависит от параметров a и
σ .
Математическое ожидание такой случайной величины равно a , а дисперсия —
σ2 .
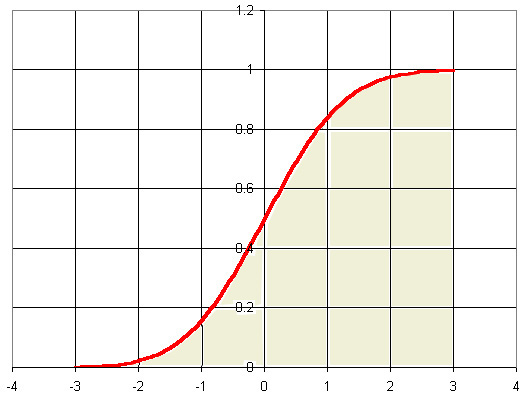
На графике показана стандартная функция с a = 0
и σ = 1 .
Причина частого появления этого закона распределения в приложениях объясняется тем, что при сложении
случайных величин очень часто распределение их суммы, рассматриваемой в качестве случайной величины,
приближается к нормальному.
В наших задачах оно встречаться не будет, но не упомянуть о нем было бы неприлично.
|
Распределение Бернулли
 Это простейшее дискретное распределение названо в честь швейцарского математика
Это простейшее дискретное распределение названо в честь швейцарского математика
Якова Бернулли старшего (1654-1705) , (еще был и младший, работавший в Петербурге).
Случайная величина распределена по Бернулли , если
она принимает всего два значения. Обычно этими значениями являются 1, вероятность которой равна
p , и 0, вероятность которого равна q = 1 − p
Математическое ожидание такой случайной величины равно p , а дисперсия —
pq .
Такой график вы, конечно, построите сами.
Закон Бернулли очень удобен для всякого рода модельных построений, он всего чуть сложнее,
чем его частный случай — бросание монеты, где p = 1/2 .
|
Биномиальное распределение
Случайная величина ξ , равная сумме n независимых одинаковых
бернуллиевских распределений, имеет биномиальное распределение . Для нее
P(ξ = k)
= Cnkpkqn − k .
Математическое ожидание такой случайной величины равно np , а дисперсия —
npq .
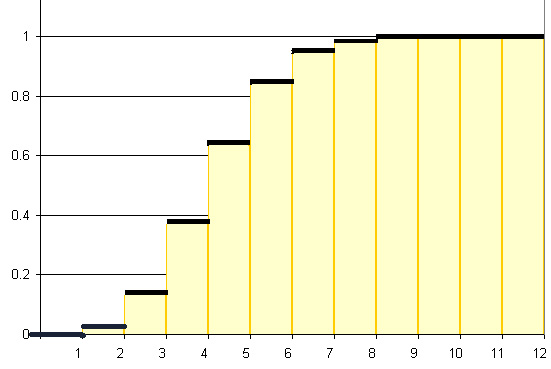 Биномиальное распределение при увеличении числа слагаемых
Биномиальное распределение при увеличении числа слагаемых n становится очень
похожим на нормальное распределение.
Нужно только подходящим образом нормировать случайную
величину: вычесть математическое ожидание и поделить на корень из дисперсии, т. е. вместо ξ
рассматривать η = (ξ - np)(npq)− 1/2 .
Если же с ростом n вероятность p уменьшается, так что
сохраняется или стабилизируется произведение np , получается другое классическое распределение.
|
Распределение Пуассона
 Это распределение предложено французским математиком
Это распределение предложено французским математиком
Симеоном Пуассоном (1781-1840) , почетным членом Петербургской Академии наук.
Случайная величина ξ имеет пуассоновское распределение , если
P(ξ = k)
= e− λλk / k! .
Математическое ожидание такой случайной величины равно λ , и дисперсия тоже
λ .
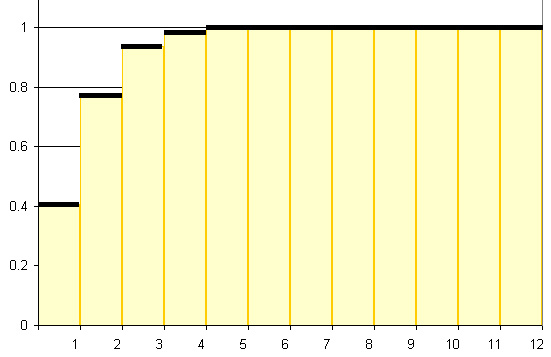
Пуассоновское распределение характерно для схемы редких событий — в которой складывается
очень много случайных величин с распределением Бернулли и очень малой вероятностью положительного
исхода у каждого.
Например, отмечалось, что количество писем, опущенных в почтовый ящик с ненадписанным конвертом
имеет пуассоновское распределение.
|
Упражнения
- Случайная величина принимает значения 0 с вероятностью 0.3, 2 с вероятностью 0.2,
4 с вероятностью 0.5. Найдите ее математическое ожидание и дисперсию.
- Две случайных величины имеют математическое ожидание 0 и дисперсию 1. В каких пределах может меняться
дисперсия их суммы. Постройте пример с наибольшим и наименьшим значением дисперсии суммы.
|
Экзаменационные вопросы
- Случайные величины и их функции распределения.
- Математическое ожидание и дисперсия. Их свойства.
- Примеры функций распределения.
|
|
 На рисунке изображена
На рисунке изображена На рисунке показан график этой функции распределения для
На рисунке показан график этой функции распределения для  На рисунке показан график этой функции распределения для
На рисунке показан график этой функции распределения для 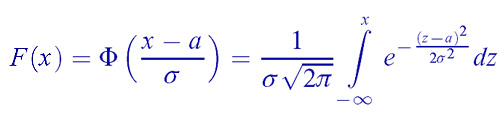


 Это простейшее дискретное распределение названо в честь швейцарского математика
Это простейшее дискретное распределение названо в честь швейцарского математика
 Биномиальное распределение при увеличении числа слагаемых
Биномиальное распределение при увеличении числа слагаемых  Это распределение предложено французским математиком
Это распределение предложено французским математиком
