| |
Лекция 1_14: Сортировки
Постановка задачи
Задача, о которой пойдет речь в этой лекции, кажется очень простой.
Совершенно не умаляя общности, можно поставить ее так:
Задано множество из n целых чисел
a[1],
a[2],
...,
a[n] .
Требуется расположить их в порядке неубывания, т.е. найти такую
подстановку
p[1],
p[2],
...,
p[n] ,
чтобы для любых i, j О 1:n,
из
i < j
следовало
a[p[i]] ≤ a[p[j]] .
Задача кажется совсем тривиальной. Например, сравнением чисел друг с другом можно
найти наименьшее число и поставить его первым. Затем найти наименьшее из оставшихся
и поставить его ... следующим. (Так говорить лучше: не вторым, а следующим. Потому что
теперь мы можем сказать так:) Это последнее действие выполним
n−1
раз, и нужное упорядочение будет получено.
К сожалению, этот способ упорядочения слишком трудоемок, приходится выполнять порядка
n2 операций, а задачу приходится
решать очень часто и с очень большими
n .
Развитие методов сортировки началось сразу же, как появились вычислительные машины,
и новые методы появляются до сих пор.
Разных методов накопилось очень много. Мы рассмотрим несколько самых важных,
а их разновидностями будем, как правило, пренебрегать.
|
Метод вставки
Будет удобно начать с маленького примера, например, с
n=8 .
Пусть
a[1:8]={5,3,8,7,13,17,6,2}.
Разобъем этот массив на начальную упорядоченную часть и неупорядоченный остаток.
Сначала упорядоченная часть состоит из всего одного элемента
5 ,
3,
8,
7,
13,
17,
6,
2.
Возьмем первый элемент остатка и включим его в упорядоченную часть, туда,
где ему полагается стоять.
Вот так:
3 ,
5 ,
8,
7,
13,
17,
6,
2.
Пришлось сравнить элементы 3 и 5 ,
и поменять их местами. Следующий элемент, 8 , мы просто
сравним с предыдущим,
и ничего трогать не будем:
3 ,
5 ,
8 ,
7,
13,
17,
6,
2.
Дальше элемент 7 сравнится с 8 ,
и продвинется вперед,
сравнится с 5 , и остановится:
3 ,
5 ,
7 ,
8 ,
13,
17,
6,
2.
Элементы
13 и
17 , сравнятся с предыдущими и не потребуют перемещений.
3 ,
5 ,
7 ,
8 ,
13 ,
17 ,
6,
2.
Элемент 6 будет сравниваться и передвигаться вперед, пока
его не остановит элемент 5 . Получим окончательно
2 ,
3 ,
5 ,
6 ,
7 ,
8 ,
13 ,
17 ,
Итак, метод вставки — это метод сортировки последовательным
расширением упорядоченной части массива. Для расширения используется очередной элемент
(первый в неупорядоченной части), который продвигается по упорядоченной части до
нахождения правильного места. Каждый шаг продвижения состоит из сравнения
с предшествующим элементом и транспозиции этих элементов в случае необходимости.
Метод вставки относится к классу методов квадратичной трудоемкости .
Среди них он не самый эффективный (например, метод выбора минимального элемента
и метод пузырька считаются более эффективными), но он наиболее удобен нам
для дальнейшего использования.
Другие квадратичные методы нет смысла рассматривать: все они слишком медленны.
|
Метод фон Неймана (метод слияния)
Метод был предложен одним из величайших математиков XX века
Джоном фон Нейманом . Это был первый алгоритм с трудоемкостью
n log2n .
В основе метода лежит операция слияния двух упорядоченных массивов
(по-английски эта операция называется merge ).
С нее и начнем.
Пусть заданы два упорядоченных массива
a[1:k] и
b[1:l]
и требуется построить упорядоченный массив
c суммарного размера
k+l .
Сравниваются первые элементы имеющихся массивов, и меньший из них записывается в начало
массива
c .
После этого действие повторяется с остатками массивов
a и
b
и с записью в очередные
элементы массива
c , так что на каждой итерации заполненная его
часть увеличивается на 1. Когда один из массивов-аргументов исчерпается, сравнение
не проводится; запись идет всегда из оставшегося массива.
Очевидно, что операция имеет трудоемкость
O(k+l).
Рассмотрим небольшой пример. Пусть
a={4,9,17,18,23}
b={6,8,14}. Рабочую информацию можно представить такой
таблицей
it |
a-rem |
b-rem |
c-res |
1 |
{4, 9,17,18,23} |
{6,8,14} |
{4 } |
2 |
{9,17,18,23} |
{6, 8,14} |
{4,6 } |
3 |
{9,17,18,23} |
{8, 14} |
{4,6,8 } |
4 |
{9, 17,18,23} |
{14} |
{4,6,8,9 } |
5 |
{17,18,23} |
{14 } |
{4,6,8,9,14 } |
6 |
{17, 18,23} |
nothing |
{4,6,8,9,14,17 } |
8 |
{23 } |
nothing |
{4,6,8,9,14,17,18,23 } |
Теперь обратимся собственно к методу фон Неймана. Он очень прост.
Вначале мы считаем, что сортируемый массив состоит из
n «упорядоченных» фрагментов,
каждый длиной 1. С помощью операции слияния соединим соседние фрагменты по два,
число фрагментов уменьшится примерно вдвое. Будем повторять это действие до тех пор,
пока число фрагментов не станет равным 1; это и будет упорядоченный массив.
Рассмотрим пример. Пусть
a={18,42,51,18,16,18,44,22,31,11,63,23,9,14} .
Имеем
a={ {18}, {42}, {51}, {18}, {16},
{18}, {44}, {22}, {31}, {11}, {63}, {23},
{9}, {14} } .
Начинаем слияния. Получающийся массив нужно писать на новое место.
b={ {18,42}, {18,51}, {16,18},
{22,44}, {11,31}, {23,63}, {9,14}, } .
На следующей итерации можно использовать старый массив.
a={ {18,18,42,51}, {16,18,22,44}, {11,23,31,63},
{9,14}, } .
b={ {16,18,18,18,22,42,44,51}, {9,11,14,23,31,63}, } .
a={ {9,11,14,16,18,18,18,22,23,31,42,44,51,63}, } .
Трудоемкость этого метода равна трудоемкости одной итерации слияния
n , умноженной на число итераций. Число итераций при
n=2k равно
k . Отсюда следует, что число итераций равно
O(log2n) .
Оставшиеся фигурные скобки роли не играют — они показывали нам границы фрагментов.
Никакой специальной информации об этих границах не требуется, они вычисляются, так как
все фрагменты (кроме, возможно, последнего имеют одинаковую длину). Иначе можно было бы
разбить исходный массив на максимальные упорядоченные фрагменты, число которых может
быть существенно меньше n . Но без такой информации
можно легко обойтись, если разбивать массив на фрагменты, упорядоченные в разных
направлениях (попеременно) и сливать фрагменты, двигаясь от начала и от конца массива.
Этот метод называется методом пилы . Рассмотрим его на том же
примере
18,42,51,18,16,18,44,22,31,11,63,23,9,14
Разобъем массив на фрагменты, двигаясь от начала и от конца к середине. Сначала найдем
участки роста значений при движении к середине. Концы участков отмечены маркерами
^| . и |^ . справа.
18,42,51,^|18,16,18,44,22,31,11,63,23,9,|^14
Дальше найдем участки убывания в оставшейся части массива. Их концы отмечены
маркерами _| . и |_ .
справа.
18,42,51,^|18,16,_|18,44,22,31,11,63,23,|_9,|^14
Потом снова участки роста
18,42,51,^|18,16,_|18,44,^|22,31,11,|^63,23,|_9,|^14
Потом снова участки убывания
18,42,51,^|18,16,_|18,44,^|22,_|31,|_11,|^63,23,|_9,|^14
Если осталось одно значение, мы с ним ничего не делаем.
На самом деле эта разметка производится в ходе работы алгоритма слияний,
а мы ее сделали для того, чтобы лучше было видно. Выполняем слияния и
получаем такой массив:
14,18,42,51,^|18,16,9,_|18,23,44,63,^||^22,|_11,|^31
Следующие массивы приводятся без комментариев
14,18,31,42,51,^|18,16,11,9,_||_18,22,23,44,|^63
14,18,31,42,51,63,^||^44,23,22,18,18,16,11,9
9,11,14,16,18,18,18,22,23,31,42,44,51,63
|
Метод Шелла
Само существование метода фон Неймана с его трудоемкостью
n log n
вызвало (особенно, если учесть, что у этого метода были недостатки)
стремление создать более удобные методы, трудоемкость которых, теоретическая
или практическая была бы на уровне метода фон Неймана.
Метод, предложенный в 1959 г. американским ученым Дональдом Шеллом, очень интересно
улучшает уже известный нам метод вставки. Интересно, что алгоритм состоит из
нескольких итераций, последняя из которых — не что иное, как сам метод
вставки, и включая метод вставки как один из своих этапов, метод Шелла
оказывается несравненно выше чистого метода вставки.
За счет чего это достигается? Метод вставки плох тем, что необходимые иногда
крупные перемещения элементов массива выполняются только мелкими шажками.
В методе Шелла этот недостаток устранен. В каждой итерации сортировки используется
свой шаг перемещения элементов, и эти шаги постепенно убывают,
доходя до единицы.
Рассмотрим этот метод все на том же примере. Мы будем выбирать для размера шага числа
вида 2r + 1 . Так как
n = 14 , самое большое из таких значений
— это 9. Для каждого шага мы сделаем отдельную таблицу. Итак,
шаг 9:
it |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
comm |
1 |
18 |
42 |
51 |
18 |
16 |
18 |
44 |
22 |
31 |
11 |
63 |
23 |
9 |
14 |
переставим |
2 |
11 |
42 |
51 |
18 |
16 |
18 |
44 |
22 |
31 |
18 |
63 |
23 |
9 |
14 |
оставим |
3 |
11 |
42 |
51 |
18 |
16 |
18 |
44 |
22 |
31 |
18 |
63 |
23 |
9 |
14 |
переставим |
4 |
11 |
42 |
23 |
18 |
16 |
18 |
44 |
22 |
31 |
18 |
63 |
51 |
9 |
14 |
переставим |
5 |
11 |
42 |
23 |
9 |
16 |
18 |
44 |
22 |
31 |
18 |
63 |
51 |
18 |
14 |
переставим |
|
11 |
42 |
23 |
9 |
14 |
18 |
44 |
22 |
31 |
18 |
63 |
51 |
18 |
16 |
пора менять шаг |
Теперь, уменьшаем шаг вдвое. Шаг 5:
it |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
comm |
1 |
11 |
42 |
23 |
9 |
14 |
18 |
44 |
22 |
31 |
18 |
63 |
51 |
18 |
16 |
оставим |
2 |
11 |
42 |
23 |
9 |
14 |
18 |
44 |
22 |
31 |
18 |
63 |
51 |
18 |
16 |
оставим |
3 |
11 |
42 |
23 |
9 |
14 |
18 |
44 |
22 |
31 |
18 |
63 |
51 |
18 |
16 |
переставим |
4 |
11 |
42 |
22 |
9 |
14 |
18 |
44 |
23 |
31 |
18 |
63 |
51 |
18 |
16 |
оставим |
5 |
11 |
42 |
22 |
9 |
14 |
18 |
44 |
23 |
31 |
18 |
63 |
51 |
18 |
16 |
оставим |
6 |
11 |
42 |
22 |
9 |
14 |
18 |
44 |
23 |
31 |
18 |
63 |
51 |
18 |
16 |
оставим |
7 |
11 |
42 |
22 |
9 |
14 |
18 |
44 |
23 |
31 |
18 |
63 |
51 |
18 |
16 |
оставим |
8 |
11 |
42 |
22 |
9 |
14 |
18 |
44 |
23 |
31 |
18 |
63 |
51 |
18 |
16 |
переставим, продолжим |
9 |
11 |
42 |
22 |
9 |
14 |
18 |
44 |
18 |
31 |
18 |
63 |
51 |
23 |
16 |
переставим |
10 |
11 |
42 |
18 |
9 |
14 |
18 |
44 |
22 |
31 |
18 |
63 |
51 |
23 |
16 |
переставим, продолжим |
11 |
11 |
42 |
18 |
9 |
14 |
18 |
44 |
22 |
16 |
18 |
63 |
51 |
23 |
31 |
оставим |
|
11 |
42 |
18 |
9 |
14 |
18 |
44 |
22 |
16 |
18 |
63 |
51 |
23 |
31 |
пора менять шаг |
Обратите внимание на четыре последних итерации. Здесь видно, что значение
продвигается вперед не один раз, а столько, сколько понадобится.
Снова уменьшаем шаг вдвое. Шаг 3:
it |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
comm |
1 |
11 |
42 |
18 |
9 |
14 |
18 |
44 |
22 |
16 |
18 |
63 |
51 |
23 |
31 |
переставим |
2 |
9 |
42 |
18 |
11 |
14 |
18 |
44 |
22 |
16 |
18 |
63 |
51 |
23 |
31 |
переставим |
3 |
9 |
14 |
18 |
11 |
42 |
18 |
44 |
22 |
16 |
18 |
63 |
51 |
23 |
31 |
оставим |
4 |
9 |
14 |
18 |
11 |
42 |
18 |
44 |
22 |
16 |
18 |
63 |
51 |
23 |
31 |
оставим |
5 |
9 |
14 |
18 |
11 |
42 |
18 |
44 |
22 |
16 |
18 |
63 |
51 |
23 |
31 |
переставим, продолжим |
6 |
9 |
14 |
18 |
11 |
22 |
18 |
44 |
42 |
16 |
18 |
63 |
51 |
23 |
31 |
оставим |
7 |
9 |
14 |
18 |
11 |
22 |
18 |
44 |
42 |
16 |
18 |
63 |
51 |
23 |
31 |
переставим, продолжим |
8 |
9 |
14 |
18 |
11 |
22 |
16 |
44 |
42 |
18 |
18 |
63 |
51 |
23 |
31 |
переставим |
9 |
9 |
14 |
16 |
11 |
22 |
18 |
44 |
42 |
18 |
18 |
63 |
51 |
23 |
31 |
переставим, продолжим |
10 |
9 |
14 |
16 |
11 |
22 |
18 |
18 |
42 |
18 |
44 |
63 |
51 |
23 |
31 |
оставим |
11 |
9 |
14 |
16 |
11 |
22 |
18 |
18 |
42 |
18 |
44 |
63 |
51 |
23 |
31 |
оставим |
12 |
9 |
14 |
16 |
11 |
22 |
18 |
18 |
42 |
18 |
44 |
63 |
51 |
23 |
31 |
оставим |
13 |
9 |
14 |
16 |
11 |
22 |
18 |
18 |
42 |
18 |
44 |
63 |
51 |
23 |
31 |
переставим, продолжим |
14 |
9 |
14 |
16 |
11 |
22 |
18 |
18 |
42 |
18 |
23 |
63 |
51 |
44 |
31 |
оставим |
15 |
9 |
14 |
16 |
11 |
22 |
18 |
18 |
42 |
18 |
23 |
63 |
51 |
44 |
31 |
переставим, продолжим |
16 |
9 |
14 |
16 |
11 |
22 |
18 |
18 |
42 |
18 |
23 |
31 |
51 |
44 |
63 |
переставим, продолжим |
17 |
9 |
14 |
16 |
11 |
22 |
18 |
18 |
31 |
18 |
23 |
42 |
51 |
44 |
63 |
оставим |
|
9 |
14 |
16 |
11 |
22 |
18 |
18 |
31 |
18 |
23 |
42 |
51 |
44 |
63 |
пора менять шаг |
Дальше нужно тоже самое выполнить с шагом 2 и с шагом 1.
Последовательности шагов могут быть разными. Например, Р. Седжвик
рекомендует следующую последовательность (мы приводим код на Си,
выложенный им в Интернете):
shellsort(itemType a[], int l, int r)
{ int i, j, k, h; itemType v;
int incs[16] = { 1391376, 463792, 198768, 86961, 33936, 13776, 4592,
1968, 861, 336, 112, 48, 21, 7, 3, 1 };
for ( k = 0; k < 16; k++)
for (h = incs[k], i = l+h; i <= r; i++) {
v = a[i]; j = i;
while (j >= h && a[j-h] > v)
{ a[j] = a[j-h]; j -= h; }
a[j] = v;
}
}
Метод Шелла считается одним из лучших методов сортировки, но все же не самым
лучшим. К самому лучшему мы сейчас перейдем.
|
Быстрая сортировка
Эта сортировка была предложена в 1962 г. английским математиком Ч. Хоаром
(Sir Charles Antony Richard Hoare).
Основная идея метода выглядит очень наивно:
Возьмем в сортируемом массиве какой-либо элемент и поставим его на то место,
где он должен стоять в упорядоченном массиве. Слева от него расположим предшествующие
элементы, а справа — следующие за ним. Затем отдельно будем сортировать левую
и правую части.
Все дело в том, что Хор предложил очень красивый способ реализации этого основного
действия. Я сейчас знаю три эффективных способа и покажу вам два.
Используется все тот же пример:
18,42,51,18,16,18,44,22,31,11,63,23,9,14 .
Будем ставить на свое место элемент 31, мы его будем называть
барьерным . Поменяем его местами с первым элементом,
вот так:
31 ,42,51,18,16,18,44,22,18,11,63,23,9,14
.
Барьерный элемент выделен. Кроме того, выделен элемент, который с барьерным
сравнивается. Если расположение барьерного и сравниваемого элементов правильно,
то происходит сдвиг — сравниваемый элемент передает свою роль элементу,
следующему по направлению к барьерному. В противном случае, как в нашем примере,
элементы сначала меняются местами, а затем сдвигается сравниваемый элемент.
Вот так:
14,42 ,51,18,16,18,44,22,18,11,63,23,9,31 .
Теперь выпишем несколько итераций
14,31 ,51,18,16,18,44,22,18,11,63,23,9 ,42 .
14,9,51 ,18,16,18,44,22,18,11,63,23,31 ,42 .
14,9,31 ,18,16,18,44,22,18,11,63,23 ,51,42 .
14,9,23,18 ,16,18,44,22,18,11,63,31 ,51,42 .
14,9,23,18,16 ,18,44,22,18,11,63,31 ,51,42 .
14,9,23,18,16,18 ,44,22,18,11,63,31 ,51,42 .
14,9,23,18,16,18,44 ,22,18,11,63,31 ,51,42 .
14,9,23,18,16,18,31 ,22,18,11,63 ,44,51,42 .
14,9,23,18,16,18,31 ,22,18,11 ,63,44,51,42 .
14,9,23,18,16,18,11 ,22,18,31 ,63,44,51,42 .
Теперь сравниваемые элементы доберутся до барьерного элемента, и сравнение прекратится
— барьерный элемент уже поставлен на правильное место. Мы можем делать то же самое
для левой и правой части отдельно.
Слабое место этого прекрасного метода — в выборе барьерного элемента. Когда выбор
падает на максимальный или минимальный элемент массива, полный просмотр массива уменьшает
размер сортируемой части всего на один элемент.
Получается так, что этим методом труднее всего сортировать уже отсортированный массив.
Есть разные способы повышения эффективности выбора. Один из них — это случайный
выбор. Очень рекомендуется выбор «среднего из трех», когда берутся,
например, крайние элементы массива и элемент, стоящий в середине массива, они
упорядочиваются, и в качестве барьера берется средний по значению. При таком выборе
гарантируется непустота и левой и правой частей.
В связи с этим интересен вариант быстрой сортировки, напоминающий подходы методам
вставки. На метод вставки нам указывает то, что массив делится на обработанную
и необработанную часть. В отличие от метода вставки обработанная часть не упорядочена,
а разделена на идущие подряд барьерный элемент, левую часть и правую часть.
На каждой итерации очередной элемент из необработанной части сравнивается с барьерным
элементом. Если он больше барьерного, то присоединяется к правой части. Для этого
правая часть просто расширяется. Если он меньше барьерного, то от меняется местами
с первым элементом правой части, а затем увеличивается размер левой части, а границы
правой части сдвигаются на единицу.
Покажем, как это происходит на том же примере
18 ,42,51,18,16,18,44 ,22,31,11,63,23,9,
14
.
Выделенные элементы переставим транспозициями в начало массива и упорядочим,
как описывалось. Чтобы левая и правая часть были виднее, окружим их фигурными
скобками
18 ,{ 14} ,
{ 44} ,18,16,18,42,22,31,11,63,23,9,51
.
Теперь начнем действия с необработанной частью. Элементы, равные барьерному,
будем присоединять поочередно к левой и правой части. Получаем
18 ,{ 14,18} ,
{ 44} ,16,18,42,22,31,11,63,23,9,51
.
18 ,{ 14,18,16} ,
{ 44} ,18,42,22,31,11,63,23,9,51
.
18 ,{ 14,18,16} ,
{ 44,18} ,42,22,31,11,63,23,9,51
.
18 ,{ 14,18,16} ,
{ 44,18,42} ,22,31,11,63,23,9,51
.
18 ,{ 14,18,16} ,
{ 44,18,42,22} ,31,11,63,23,9,51
.
18 ,{ 14,18,16} ,
{ 44,18,42,22,31} ,11,63,23,9,51
.
18 ,{ 14,18,16,11} ,
{ 18,42,22,31,44} ,63,23,9,51
.
18 ,{ 14,18,16,11} ,
{ 18,42,22,31,44,63} ,23,9,51
.
18 ,{ 14,18,16,11} ,
{ 18,42,22,31,44,63,23} ,9,51
.
18 ,{ 14,18,16,11,9} ,
{ 42,22,31,44,63,23,18} ,51
.
18 ,{ 14,18,16,11,9} ,
{ 42,22,31,44,63,23,18,51}
.
Осталось вставить барьерный элемент между левой и правой частью
{ 9,14,18,16,11} ,18 ,
{ 42,22,31,44,63,23,18,51}
.
Метод, используемый в промышленных системах, почти не отличается от изложенного.
Отличие в том, что все мелкие части не сортируются по отдельности, алгоритм завершается
одним «прогоном» метода вставки по всему массиву. Кроме того, считается
целесообразным в случаях, когда несколько раз подряд барьерный элемент находится
неэффективно, вызывать какой-либо запасной алгоритм.
Правило «разбрасывания» элементов, равных барьерному, защищает нас в случае,
когда в массиве оказалось много одинаковых элементов.
|
Иерархическая сортировка
Если мы знаем, что быстрая сортировка является сейчас лучшей, то зачем же рассматривать
еще какие-то?
Сортировка, с которой мы знакомимся сейчас, интересна по многим причинам.
Во-первых, это большое теоретическое достижение: она имеет такую же трудоемкость, как сортировка
фон Неймана, и не требует дополнительной памяти.
Во-вторых, очень поучительно, что этот прекрасный теоретический результат не дает прямого
практического результата: сортировка существенно уступает в скорости быстрой сортировке,
так что связь хорошей теории с хорошей практикой сложнее, чем кажется.
Этот метод называется Heapsort , а по-русски сортировка кучей или
иерархическая сортировка . В ней используется специальный объект, называемый
Heap (куча). Роль кучи играет уже встречавшееся нам
двоичное дерево , причем в самом простом варианте, с одинаковыми или почти
одинаковыми длинами расстояний от корня до листьев.
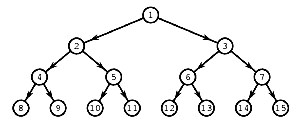Рассмотрим полное двоичное дерево с ветвями высоты
k .
Такое дерево имеет
2k+1 − 1
вершин. Действительно, корневая вершина образует как бы нулевой слой этого дерева,
а далее в каждом горизонтальном слое число вершин вдвое больше, чем в предыдущем, и слой
k
содержит
2k
вершин. Если перенумеровать вершины сверху вниз и слева направо, как показано
на рисунке, то легко убедиться (докажите сами!),
что вершина с номером
s
соединяется с вершинами
2s
и
2s+1
из следующего слоя.
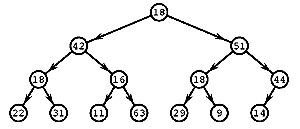Иерархическая сортировка основана на этом способе нумерации.
Каждому индексу
iО 1:n
сопоставляется вершина, и элементы массива
a[1:n]
могут рассматриваться как вершины двоичного дерева (в нижнем слое можно
удалить несколько вершин). На рисунке показано дерево,
соответствующее массиву из многократно использованного примера.
В терминах этого дерева и происходит сортировка массива; простая
арифметическая связь номеров соединенных вершин позволяет связать
вершины дерева с элементами массива.
Сортировка состоит из двух фаз. Первая фаза обеспечивает
иерархическую упорядоченность массива: перестановкой элементов
мы добиваемся того, чтобы значение в каждой вершине было хуже,
чем у детей. Для этого используется операция «утапливания»
элемента: текущий элемент сравнивается с худшим из элементов-детей и,
если тот хуже, они меняются
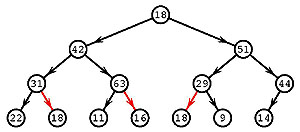местами; на новом месте операция для текущего
элемента повторяется.
Так утапливается каждый элемент начиная от
наибольшего номера, не превосходящего
n/2 .
и кончая 1. В нашем примере 7-й элемент (44) утапливать не нужно,
6-й (11) меняется с 12-м (29), 5-й (16) с 11-м (63), 4-1 с 9-м (31).
Получается граф, изображенный на рисунке справа.
Затем 3-й элемент утапливать не нужно,
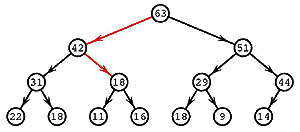а 2-й меняется с 5-м (это мы показывать не будем.
Наконец, 1-й элемент меняется
со 2-м (63), а затем с 5-м (43). Этим завершается
первая фаза. Результат виден на рисунке слева.
Выпишем текущее состояние сортируемого массива
{63,42,51,31,18,29,44,22,18,11,16,18,9,14} .
Вторая фаза сортировки состоит из последовательного выполнения
следующих действий: взять самый худший элемент (он сейчас на первом
месте, а должен быть на последнем), поменять его местами с последним,
сократить на единицу число вершин в дереве, «отцепив» последний
элемент, утопить верхний элемент дерева, чтобы восстановить
иерархическую упорядоченность. Так, после установки значения 63 на
последнее место в массиве, а стоящего там значения 14 на первое место
и его утапливания, получаем
{51 ,42,44 ,31,18,29,14 ,
22,18,11,16,18,9; 63} .
Траектория утапливания выделена цветом. Отсортированная часть массива, уже не включаемая в дерево ,
отделена точкой с запятой, чтобы было виднее.
|
Программная реализация сортировок
Все перечисленные алгоритмы сортировки достаточно просты и легко программируются,
но все же хочется не писать их каждый раз заново.
Действительно, если мы взглянем на образцово написанную процедуру
shellsort , приведенную выше, и захотим использовать ее
в своем контексте, мы легко увидим в ней подлежащий уточнению тип данных
itemType , но не сразу увидим действия над этими данными,
которые мы должны обеспечить — операцию сравнения элементов этого типа,
спрятавшуюся в операции > , и совсем непростую операцию
присваивания.
Операция присваивания может оказаться сложной из-за того, что отдельные элементы
данного типа (например, если это строки) могут оказаться разного размера.
Можно прямо сказать, что при сортировке записей переменного размера проще не
переставлять сами эти записи, а создать массив их адресов или
указателей .
Например, чтобы упорядочить слова фразы
.........1.........2.........3.........4.........5.........6.........7.........8
12345678901234567890123456789012345678901234567890123456789012345678901234567890
все перечисленные алгоритмы сортировки достаточно просты и легко программируются
мы составим массив адресов, в который вначале запишем
01,05,19,29,40,51,58,60,66
а результат при лексикографическом упорядочении получим в виде
19,01,40,58,60,05,66,51,29
— адреса просто переставляются (они, как правило, и короче слов), а сравнение адресов,
конечно же, выполняется не по их значениям, а по словам, которые в этих адресах
находятся.
Операция сравнения может быть очень разнообразной. Например, при составлении
алфавитного указателя в книге нас может не устраивать сравнение по кодам символов.
Посмотрите, как при лексикографическом сравнении будут упорядочены несколько слов
и последовательностей символов
125 32 =11
Euler
Wald
\begin \new
`under and
integer
Ёлка
АВЛ Аббат МВД д'Артаньян дама
Здесь числа и некоторые специальные знаки предшествуют буквам,
все прописные буквы предшествуют строчным, латиница предшествует кириллице,
буква Ё и буквы украинского алфавита (например, буква Ґ )
предшествуют букве А .
В некоторых изданиях мы видим, что указатель был сделан именно так.
Между тем, издательскими правилами диктуется иной порядок:
- Прописные и строчные буквы равноправны,
- Буква
Ё идет после Е ,
- Кириллица предшествует латинице,
- Буквы предшествуют специальным символам.
Оказывается в рамках однобайтовой кодировки (и одной кодовой таблицы) легко добиться
почти всех требуемых эффектов. Достаточно сделать таблицу rank из 256 чисел,
отображающую
используемые символы в ранги, и при сравнении символов пользоваться этой таблицей:
i предшествует j ,
если rank(j) > rank(i)
Конечно, такой таблицей все проблемы не решаются. В частности, очень неудобно, что цифры,
входящие в состав слова, трактуются как символы, и, скажем, строка
школа_259 предшествует строке школа_45 .
Мы часто встречаемся с таким неудобством при просмотре файлов: например, если мы сканируем текст
и нумеруем страницы подряд, то файл
page_10 предшествует файлу page_2
(при большом числе файлов их иногда даже трудно найти, — так что лучше сразу об этом
подумать и писать числа с нужным числом нулей: page_010 ,
page_002 ).
Часто приходится сортировать данные по составному ключу : отдельные характеристики
(ключи) рассматриваются как своего рода символы для лексикографического сравнения. Например, упорядочивая
список студентов, мы можем располагать их сначала по курсам, потом по фамилиям, потом по группам,
потом по именам, потом по отчествам. Практичную сортировку по трем таким ключам вы можете
увидеть и использовать в системе Excel.
|
Поразрядная сортировка
Вот сортировка, сделанная по идеям сортировки перфокарт .
(Вы не знаете, что такое перфокарта?
Посмотрите картинку.) Начнем опять с примера,
все того же.
Воспользуемся тем, что мы сортируем двухзначные неотрицательные дясятичные числа
(мы даже 9 записали с двумя знаками)
18,42,51,18,16,18,44,22,31,11,63,23,09,14 .
Просматривая эти числа, от первого до последнего, разложим их на 10 кучек,
в зависимости от последней цифры. Получим таблицу
цифра | 0 | 1 |
2 | 3 | 4 |
5 | 6 | 7 |
8 | 9 |
кучка | |
51
31
11 | 42
22 |
63
23 | 44
14 |
| 16 |
| 18
18
18 |
09 |
и составим из этих кучек массив. Вот так
51,31,11,42,22,63,23,44,14,16,18,18,18,09.
Этот массив снова разложим по кучкам, но уже по старшей цифре
цифра | 0 | 1 |
2 | 3 | 4 |
5 | 6 | 7 |
8 | 9 |
кучка | 09 | 11
14
16
18
18
18 |
22
23 | 31 | 42
44 |
51 | 63 | |
|
|
Видно, что массив, сложенный из этих кучек, будет уже отсортирован.
Если бы разрядность сортируемых чисел была больше, нам пришлось бы проводить
такое раскладывание больше раз, но процедура упорядочения была бы такой же простой.
Сортировка массива из
n чисел c максимальной разрядностью
k
будет иметь трудоемкость O(kn) —
она линейна по
n при фиксированном
k .
Сортировочная машина для перфокарт делала фактически то же самое. На специальном
индикаторе можно было выбрать колонку перфокарты, по которой анализировались
поступающие в сортировку карты мз колоды перфокарт, и очередная карта попадала
в один из 10 (на самом деле, из 12, я упрощаю) карманов. Затем кучки из карманов
складывались в одну колоду.
Оказалось, что с уходом со сцены перфолкарт и сортировочной машины, идея не умерла:
в современном компьютере такому методу находится достаточно применений. При этом
кучки программируются с помощью цепных списков, у которых запоминается начало и конец,
и элементы прибавляются в конец, а для складывания кучек нужно просто сцепить
соответствующие им цепные списки.
|
Построение суффиксного массива
Пусть задана строка
s , которая в конце дополнена
«флажковым символом» (sentinel). Этот символ больше нигде
в строке не содержится и при лексикографическом упорядочении предшествует
любому другому символу. Обозначим число символов в этой расширенной
строке через
n .
Нам нужно расставить в лексикографическом порядке все
n
суффиксов этой строки. Так как суффикс можно задать номером начального символа,
то информация об этих суффиксах очень компактна: ищется просто подстановка
множества
1:n .
Сама эта подстановка и называется суффиксным массивом .
Несколько лет назад были разработаны чрезвычайно эффективные методы
построения суффиксного массива. Рассмотрим один из них.
Рассмотрение будем вести на примере. Для флажкового символа принято использовать
знак доллара. В качестве строки возьмем:
.........1.........2.........3.........4.........5.
123456789012345678901234567890123456789012345678901
бах-бах-тарабах-бах-бах-тарабах-плюх-раба-баба-бах$
Подсчитаем частоты появления символов в строке:
$ 1 1
- 9 10 а 15
25 б 10 35
л 1 36
п 1 37 р
3 40 т 2
42 х 8 50
ю 1 51
Данные состоят из троек: (символ, частота, накопленная частота). Накопленные частоты
можно использовать для разметки суффиксного массива
|01|02|03|04|05|06|07|08|09|10|11|12|13|14|15|16|17|18|19|20|21|22|23|24|25|
[51X04|08|16|20|24|32|37|42|47X02|06|10|12|14|18|22|26|28|30|39|41|44|46|49]
|26|27|28|29|30|31|32|33|34|35|36|37|38|39|40|41|42|43|44|45|46|47|48|49|50|51|
[01|05|13|17|21|29|40|43|45|48X34X33X11|27|38X09|25X03|07|15|19|23|31|36|50X35]
На первом месте, естественно, стоит суффикс, состоящий из флажкового символа.
Этот суффикс уже занимает свое место в упорядочении.
Затем идет группа из 9 суффиксов, начинающихся с символа -.
|02|03|04|05|06|07|08|09|10|
X04|08|16|20|24|32|37|42|47X
X05|09|17|21|25|33|38|43|48X
По правилам лексикографического сравнения эти суффиксы упорядочены так же, как их продолжения,
записанные в третьей строке. Суффиксы 05, 17, 21, 43, 48 принадлежат группе 26:35,
суффиксы 09 и 25 группе 41:42, суффикс 33 стоит на 37 месте, суффикс 38 в группе 38:40.
Эта информация позволяет нам уточнить упорядочение в этой группе, сделав разбиение
более мелким
|02|03|04|05|06|07|08|09|10|
X04|16|20|42|47X32X08|24X37X
X05|17|21|43|48X33X09|25X38X
Аналогично поступаем с группами 11:15, 16:25, 26:35, 39:40, 41:42, 43:50. Получается такое разбиение
|01|02|03|04|05|06|07|08|09|10|11|12|13|14|15|16|17|18|19|20|21|22|23|24|25|
[51X04|16|20|42|47X32X08|24X37X41|46X12|28|39|44X10|26X02|06|14|18|22|30X49]
|26|27|28|29|30|31|32|33|34|35|36|37|38|39|40|41|42|43|44|45|46|47|48|49|50|51|
[40|45X43X01|05|13|17|21|29|48X34X33X11|27|38X09|25X50X03|15|19|31X23|36X07X35]
Смотрите, как много одноэлементных групп! Вместе с тем, две группы, 38:40 и 41:42, при этом
уточнении не распались. Это естественно — за символами р и т продолжения одинаковы.
Теперь в каждой группе совпадают префиксы глубины 2 (а в некоторых случаях уже и глубже),
что нужно учесть при сравнении. Анализируем группу 02:06
|02|03|04|05|06|
X04|16|20|42|47X
X06|18|22|44|49X
Суффиксы 06, 18, 22, 49 принадлежат группе 17:25, а суффикс 44 группе 13:16, значит, он
предшествует всем остальным
|02|03|04|05|06|
X42X04|16|20|47X
X44X06|18|22|49X
Аналогично поступаем с группами 08:09, 11:12, 13:16, 17:18, 19:24, 26:27, 29:35,
38:40, 41:42, 44:47, 48:49. Получается такое разбиение
|01|02|03|04|05|06|07|08|09|10|11|12|13|14|15|16|17|18|19|20|21|22|23|24|25|
[51X42X04|16|20|47X32X08|24X37X41X46X39X44X12|28X10|26X02|14|18X30X06|22X49]
|26|27|28|29|30|31|32|33|34|35|36|37|38|39|40|41|42|43|44|45|46|47|48|49|50|51|
[45X40X43X48X01|13|17|29X21X05X34X33X11|27|38X09|25X50X15X19X03X31X36X23X07X35]
Обеспечено совпадение на глубину 4. Анализируем группу 03:06
|03|04|05|06|
X04|16|20|47X
X08|20|24|51X
Суффикс 51 предшествует всем, 08 и 24 находятся в одной группе, 20 им предшествует. Надо анализировать
группы 08:09, 15:16, 17:18, 19:21, 23:24, 30:33, 38:40, 41:42. Получилось разбиение
|01|02|03|04|05|06|07|08|09|10|11|12|13|14|15|16|17|18|19|20|21|22|23|24|25|
[51X42X47X16X04|20X32X08|24X37X41X46X39X44X12X28X10X26X49X02X14X18X30X06X22]
|26|27|28|29|30|31|32|33|34|35|36|37|38|39|40|41|42|43|44|45|46|47|48|49|50|51|
[45X40X43X48X13|17X05X29X21X05X34X33X38X27X11X09X25X50X15X19X03X31X36X23X07X35]
Осталось три группы по два элемента: 05:06, 08:09, 30:31. Во всех этих группах элементы
уже стоят правильно
|01|02|03|04|05|06|07|08|09|10|11|12|13|14|15|16|17|18|19|20|21|22|23|24|25|
[51X42X47X16X04X20X32X08X24X37X41X46X39X44X12X28X10X26X49X02X14X18X30X06X22]
|26|27|28|29|30|31|32|33|34|35|36|37|38|39|40|41|42|43|44|45|46|47|48|49|50|51|
[45X40X43X48X13X17X05X29X21X05X34X33X38X27X11X09X25X50X15X19X03X31X36X23X07X35]
|
Упражнения
- Напишите несколько (10-20) целых чисел из диапазона 10:99 и упорядочите их всеми
описанными способами.
|
Экзаменационные вопросы
- Сортировка вставкой.
- Сортировка слиянием (фон Неймана).
- Сортировка Шелла.
- Быстрая сортировка.
- Иерархическая сортировка.
- Поразрядная сортировка.
- Построение суффиксного массива.
|
|