Лекция 7: Теория вероятностей. Моделирование случайных распределений

Постановка задачи

Вычислительные машины дали нам принципиально новый способ вычислений: моделируется случайная величина и проводится серия наблюдений. По статистике наблюдений можно оценить параметры этой величины.

Обязательной составляющей этого подхода является моделирование случайных величин с нужным законом распределения. Мы рассмотрим в этой лекции только вопросы моделирования дискретных распределений.

Дискретное равномерное распределение

Для начала рассмотрим случай, когда все исходы дискретного распределения имеют одну и ту же вероятность. Если число исходов равно n, то эта вероятность равна, очевидно, 1 / n.

Разделим отрезок [0, 1] на n равных частей, перенумерованных от 0 до n − 1: I₀, I₁, ... , I_{n − 1}. Далее рассматривается равномерно распределенная случайная величина ξ и функция от нее η = h(ξ) = floor(ξ × n), паскалевская процедура floor(x) вычисляет наибольшее целое число, не превосходящее x.

Легко видеть, что случайная величина η принимает значения от 0 до n − 1 и вероятность наступления каждого исхода одна и та же.

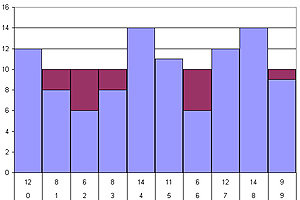Вот график, показывающий результаты 100 наблюдений этой случайной величины с датчиком случайных чисел системы Excel. Мы видим, что наблюдаемые частоты (голубые столбики, снизу написаны соответствующие им частоты и значения случайной величины) довольно сильно отличаются от теоретически ожидаемых значений (лиловые столбики).

При увеличении числа экспериментов точность, вообще говоря, повысится. Посмотрим, что получилось, когда мы довели число наблюдений до 400.

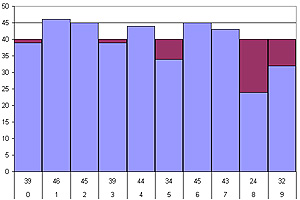Как видите, у одного из значений получилось такое же значительное относительное (т. е. долевое) отклонение, а, значит, в абсолютных величинах оно увеличилось в четыре раза.

Произвольное дискретное распределение

Пусть теперь задана случайная величина, принимающая несколько значений с неравными вероятностями. В качестве примера возьмем случайную величину, принимающую значения


x   A   B   C   D   E

100 P(x) 33 13 17 11 26

Здесь появляется небольшое затруднение: формировать функцию h(ξ), определяющую интервал, в который попало выданное датчиком значение ξ, стало сложнее. Конечно, мы можем расположить интервалы подряд, вычислить для каждого интервала левую и правую границы,


x   A   B   C   D   E

100 P(x) 33 13 17 11 26

L 0 33 46 63 74

R 33 46 63 74 100

а дальше перебирать интервалы подряд, пока не найдем нужный интервал.

Легко подсчитать распределения числа проверок в такой схеме: одна проверка произойдет с вероятностью p₀, две с вероятностью p₁, и так далее. С вероятностью p_{n − 2} + p_{n − 1} число проверок будет равно n − 2.

Число проверок становится у нас случайной величиной. Обозначим ее через μ и найдем ее математическое ожидание

      Eξ = 1 · p₀ + 2 · p₁ + ... + (n − 2) · (p_{n − 2} + p_{n − 1}).

Вспоминая экстремальную задачу, которая нам встретилась при изучении перестановок, можем сразу внести в эту схему усовершенствование: лучше располагать вероятности по убыванию, это обеспечит минимум математического ожидания. Вот так:


x   A   E   C   B   D

100 P(x) 33 26 17 13 11

L 0 33 59 76 89

R 33 59 76 89 100

Дальнейшее усовершенствование функции h(ξ) основывается на так называемой дихотомической схеме поиска. Дихотомия — это деление на две части.

Все множество исходов, уже упорядоченных по вероятностям, делится на две части так, чтобы вероятности попадания в обе части были примерно одинаковы. В нашем примере это части {A,E} и {C,B,D}.

Части, содержащие более одного исхода, снова делятся примерно пополам, и это деление продолжается до тех пор, пока в нем есть нужна. Таким образом, {A,E} разбивается на A и E, {C,B,D} разбивается на C и {B,D}, затем последнее окончательно разбивается на B и D. В такой схеме на поиск B и D тратится по три попытки, а на все остальные исходы по две.

Мы будем более подробно заниматься дихотомическим поиском и его оптимизацией на следующей лекции, а сейчас рассмотрим еще один метод моделирования дискретной случайной величины с неожиданной и очень эффективной идеей.

Метод Уолкера

Идея Уолкера заключалась в том, что за основу бралась схема моделирования дискретного равномерного распределения и предлагалось делать в этой схеме поправки на неравномерность.

Саму идею полезно посмотреть вначале на одной поправке. В качестве примера возьмем распределение с пятью исходами

x A B C D E

100 P(x) 20 13 20 20 27

Распределение отличается от равномерного всего в двух случаях — в исходе B на 0.07 меньше, в E на столько же больше. Легко изменить схему определения индекса, чтобы лишняя вероятность передавалась от исхода B исходу E. Действительно, потребуем, чтобы при 0.33 < ξ < 0.40 вырабатывался вместо исхода B исход E.

Очень простое изменение! У нас исход B стал в каком-то смысле донором дополнительной вероятности, а исход E ее реципиентом.

Такую поправку можно было бы делать у каждого исхода: нам достаточно завести массив порогов (по одному на каждого донора) и массив реципиентов. Возникает вопрос: какие распределения можно моделировать по такой схеме доноров и реципиентов? Оказывается, любые! Это мы сейчас и докажем, просто предъявив алгоритм построения системы барьеров.

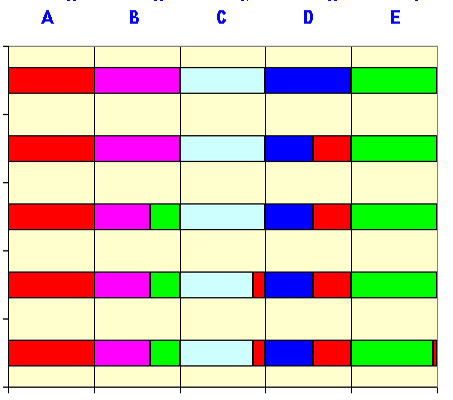
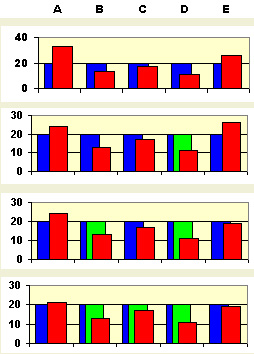
Возьмем прежний пример с пятью исходами. Сначала выберем в качестве донора исход D (самый богатый донор) и сопоставим ему в качестве реципиента исход A (самый нуждающийся). Излишки донора не превосходят средней доли, и реципиент все эти излишки может принять. Во второй строке диаграмм изображен результат передачи. Исход D в дальнейшем перераспределении не участвует. Теперь в качестве донора выбирается исход B, который передает свои излишки исходу E, причем, как видно по третьей строке, тот сам становится донором. Дальше C передаст свои излишки A, а затем то же сделает и E.

Очевидно, что такие перераспределения возможны при любом наборе вероятностей.

Упражнения

Рассчитайте схему моделирования для случайной величины, принимающей 5 значений с вероятностями 0.70, 0.15, 0.10, 0.03 и 0.02.

Экзаменационные вопросы

Моделирование дискретных распределений. Линейная и дихотомическая схема поиска интервала.

Моделирование дискретных распределений. Метод Уолкера.