Лекция 5: Теория вероятностей. Основные определения
Предмет лекции
Сейчас не требуется много говорить о случайности и ее имитации в компьюерах, так как, вероятно,
каждый из нас играл в компьютерные игры, в том числе в карточные.
 В основе каждой такой игры — случайный расклад колоды карт, в которой мы с равным шансом
ожидаем любой из 52! перестановок карт в колоде.
В основе каждой такой игры — случайный расклад колоды карт, в которой мы с равным шансом
ожидаем любой из 52! перестановок карт в колоде.
(Напомним, 52! = 80658175 1709438785 7166063685 6403766975 2895054408 8327782400 0000000000 .)
Изучением закономерностей случайных явлений занимается теория вероятностей .
У вас будет в дальнейшем основательный курс теории вероятностей, но некоторые элементарные
представления о ней нам потребуются прямо сейчас, поэтому нам придется забежать вперед и
уделить ей некоторое время.
Теория вероятностей вводит и изучает количественную меру ожидаемой случайности. У нас
имеется чувство возможности того или иного исхода. Мы считаем, что маловероятны заморозки
в июле, четыре туза на одной руке в игровом раскладе, и т. д. А при бросании монеты считаем,
что она с равными шансами упадет вверх гербом или решеткой. Равные шансы мы приписываем
и любому числу очков на игральной кости.
|
Элементарная теория вероятностей
Элементарная теория вероятностей началась с переписки двух замечательных математиков —
Блеза Паскаля, имя которого упоминалось на прошлой лекции, и Пьера Ферма, имя которого до сих пор треплется
досужими журналистами. Конечно, мы не следуем их работам в точности.
В основе элементарной теории вероятностей лежит понятие пространства элементарных событий .
Пусть задано непустое конечное множество S , элементы которого называются
элементарными событиями . Они считаются равноправными,
в том смысле, что их исходы равновозможны .
Подмножества S называются просто событиями .
Для каждого события A М S определяется
мера P(A) возможности его появления,
называемая вероятностью A .
Эта мера обладает следующими свойствами:
- Для любого
A выполняются неравенства
0 £ P(A) £ 1 .
-
P(S) = 1 . Множество S
называется достоверным событием.
-
P(Ж ) = 0 . Пустое множество Ж
называется невозможным событием.
- Если
A М B , то
P(A) £ P(B) .
- Если множества
A и B дизъюнктны,
т. е. A З B = Ж , то
P(A И B) = P(A) + P(B) .
Для рассматриваемой схемы вероятность события A определяется как число
содержащихся в нем элементарных событий, деленное на общее число событий в S .
|
Формула полной вероятности
Пусть задано разбиение множества S на подмножества
B1 , B2, …, Bk .
Для любого множества A справедливо равенство
P(A) =
Σi P(A З Bi) .
Эта формула и называется формулой полной вероятности .
Она нужна для того, чтобы вычислять вероятности событий по частям —
вероятности совмещения событий бывает считать проще чем исходные события.
Формула становится еще более удобной, если ввести понятие условной вероятности.
|
Условные вероятности и независимость событий
Пусть B — событие, имеющее положительную вероятность.
Для любого множества A определим
P(A|B) =
P(A З B) / P(B) .
Эта величина называется вероятностью A при условии B .
Легко видеть, что при фиксированном условии B величины
P(A|B) обладают всеми свойствами вероятности.
В том случае, если P(A|B) = P(A)
(говорят: если условная вероятность равна безусловной),
события A и B называются независимыми .
При числе событий, большем 2, различают попарную независимость событий
и их независимость в совокупности .
|
Пример С. Н. Бернштейна
Академик Сергей Натанович Бернштейн (1880 - 1968) предложил простой пример, по которому легко
увидеть различия этих двух форм независимости событий:
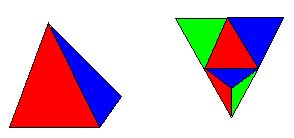 Рассмотрим тетраэдр (на рисунке показан его вид в перспективе и развертка), у которого
три грани выкрашены каждая в свой цвет, а четвертая в смесь цветов.
Рассмотрим тетраэдр (на рисунке показан его вид в перспективе и развертка), у которого
три грани выкрашены каждая в свой цвет, а четвертая в смесь цветов.
Какова вероятность события R — на нижней грани есть красный цвет?
Очевидно, 2 / 4 = 1 / 2 .
Также для события B — синий цвет и G — зеленый цвет.
Вероятности событий R З B
и им подобных равны 1 / 4 , так что события R ,
B , G — попарно независимы.
Но P(R З B З G)
= 1 / 4 , а не 1 / 8 , как хотелось бы.
|
Формула Байеса
Вернемся теперь к формуле полной вероятности и преобразуем ее, используя условные вероятности
P(A) =
Σi P(A | Bi)
· P(Bi) .
 Эта формула также называется формулой полной вероятности. Из нее удобно получить еще одну
формулу, которая называется
Эта формула также называется формулой полной вероятности. Из нее удобно получить еще одну
формулу, которая называется формулой Байеса (1764).
Справа помещен портрет Томаса Байеса (Thomas Bayes, 1702-1761). По датам видно,
что формула Байеса стала известной уже после его смерти. При жизни он ничего не публиковал,
но тем не менее в 1742 г. был избран членом Лондонского Королевского общества.
Сейчас термин байесовский распространен необычайно широко, но об этом немного позже.
Пока напишем формулу для еще одной условной вероятности
P(Bi|A) =
P(A З Bi) / P(A)
и преобразуем ее, подставляя известные нам выражения в ее числитель и знаменатель.
Получаем
P(Bi|A) =
P(A | Bi) · P(Bi)
/ Σk
P(A | Bk) · P(Bk) .
Формула Байеса используется для оценки влияния эксперимента на вероятности условий.
Рассмотрим простой пример. Имеется две колоды карт, в 52 листа и в 36 листов.
Выбирается одна из колод (с равной вероятностью) и из нее вытаскивается случайно одна карта.
Меняет ли информация об этой карте наши представления о выбранной колоде?
Да! Если выбрана карта, которой нет в К-36, то выбрана К-52. Это очевидно.
А если выбрана карта, которая есть в К-36. Вероятности по-прежнему равны, или что-то изменилось?
Давайте обсудим это.
Представьте себе, что мы много раз проводите один и тот же эксперимент — вытаскивали карту из
колоды (а потом возвращали). Мы сделали это 1000 раз, и каждый раз получали карту из К-36. Повлиял ли
этот длинный эксперимент на наши предположения? Скорее всего, мы ответим да. Не может быть (нет,
маловероятно), чтобы при тысяче экспериментов ни разу не появилась карта из продолжения колоды.
А если мы сделаем только 100 попыток? Или 50? Неужели есть такой порог, при котором наши представления
изменяются? Конечно же, нет. Просто при каждой попытке вероятность изменяется очень мало.
Так давайте же считать. Формула Байеса и дает нам такую возможность.
Введем события
B36 — выбрана колода К-36.
B52 — выбрана колода К-52.
A — из колоды вынута карта ª 8 .
Очевидно имеем
P(B36|A) =
P(A | B36) · P(B36)
/ (P(A | B36) · P(B36)+
P(A | B52) · P(B52)
) .
Легко устанавливаем, что
P(B36) = 1/2 ,
P(B52) = 1/2 ,
P(A | B36) = 1/36 ,
P(A | B52) = 1/52 .
Подставляя, получаем
P(B36|A) =
(1/2) · (1/36)/ ( (1/2) · (1/36) + (1/2) · (1/52)
) = 36/88 = 9/22 .
И от одного эксперимента вероятность уменьшилась, хотя и немного.
|
Дополнительная литература

Джерси Нейман является одним из крупнейших специалистов прошлого века по теории
вероятностей и ее статистическим приложениям. Он родом из Российской Империи (Джерси = Юрий),
работал в Калифорнийском университете в Беркли, неоднократно приезжал в Советский Союз.
|

На обложке написана цифра 1, это первый том из двух.
Вилли Феллер — один из крупнейших американских специалистов по теории вероятностей.
Когда я в 1953 г. переходил на матмех, Ю. В. Линник рекомендовал мне первый том Феллера на лето.
Это было замечательное чтение.
Второй том был написан и переведен много позднее. После этого и первый том был издан заново,
причем были восстановлены лакуны первого издания, вызванные так называемой
лысенковщиной — подавлением научного подхода к биологии (и, в частности,
использования математических методов) средствами государственного репрессивного аппарата.
|

Братья-близнецы Акива Моисеевич и Исаак Моисеевич Ягломы работал в Москве, много писали книжек
для школьных математических кружков. Теперь одних уж нет (И.М.), а те (А.М.) —
далече. Но прекрасная книжка осталась и не имеет замены.
|
Упражнения
- В урне 10 красных и 6 белых шаров. Случайно достали два шара. Найдите вероятность того, что оба шара белые.
- Найдите вероятность того, что при доставании из урны 5 шаров последний шар будет белый.
|
Экзаменационные вопросы
- Вероятность. Основные определения и свойства.
- Условные вероятности. Формула полной вероятности.
- Формула Байеса.
|
|
 В основе каждой такой игры — случайный расклад колоды карт, в которой мы с равным шансом
ожидаем любой из 52! перестановок карт в колоде.
В основе каждой такой игры — случайный расклад колоды карт, в которой мы с равным шансом
ожидаем любой из 52! перестановок карт в колоде. Рассмотрим тетраэдр (на рисунке показан его вид в перспективе и развертка), у которого
три грани выкрашены каждая в свой цвет, а четвертая в смесь цветов.
Рассмотрим тетраэдр (на рисунке показан его вид в перспективе и развертка), у которого
три грани выкрашены каждая в свой цвет, а четвертая в смесь цветов. Эта формула также называется формулой полной вероятности. Из нее удобно получить еще одну
формулу, которая называется
Эта формула также называется формулой полной вероятности. Из нее удобно получить еще одну
формулу, которая называется 

